In ECET 2026 Mathematics, Definite Integrals and Area under Curves are highly important. Almost every year, questions appear from this topic. With proper understanding and practice, you can score easy marks.
📘 Concept Notes – Area Under Curves
🔹 Definition
The area under a curve 
between limits 
and 
is given by the definite integral:
🔹 Basic Cases
- Area under x-axis:
- If
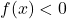in the interval, the integral gives negative value. - Actual area =
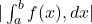
- If
- Area between two curves:
If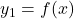
and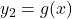 
, then: 
(where
)
🔹 Important Formulas
- Area under curve:
Area between curve and x-axis:
Area between two curves:
Area in polar coordinates:
For 
from 
to 
:
📐 Example 1
Find the area under the curve 
between 
and 
.
![A = \left[ \dfrac{x^3}{3} \right]_{0}^{2} = \dfrac{8}{3}](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-4dc3c823da3731033a8cf2a717888bca_l3.png "Rendered by QuickLaTeX.com")
So area = 
.
📐 Example 2
Find the area between the curves 
and from 
to 
.
![A = \left[ \dfrac{x^2}{2} + x - \dfrac{x^3}{3} \right]_{0}^{1}](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-3474371d70d096603b90e4ac82ed38d6_l3.png "Rendered by QuickLaTeX.com")
So area = 
.
🔟 10 Expected MCQs – ECET 2026
Q1. The area under the curve from to is given by:
A) 
B) 
C) 
D) None
Q2. If 
in [a, b], then actual area is:
A) Negative integral
B) Zero
C) 
D) None
Q3. Area between and 
is:
A) 
B) 
C) 
D) None
Q4. Area under from 0 to 1 is:
A) 
B) 
C) 1
D) 
Q5. Area in polar coordinates is given by:
A) 
B) 
C) 
D) None
Q6. Area under 
from 
to 
is:
A) 1
B) 0
C) 2
D) -2
Q7. If 
, then A = ?
A) 0
B) 4/3
C) 2
D) 8/3
Q8. Area between y=x and y=x² from 0 to 1 is:
A) 1/3
B) 2/3
C) 1/6
D) 5/6
Q9. For 
between 0 and 2, area = ?
A) 1
B) 2
C) 3
D) 2
Q10. Area between 
and x-axis from 0 to 
is:
A) 0
B) 1
C) 2
D) None
✅ Answer Key
| Q.No | Answer |
|---|---|
| Q1 | B |
| Q2 | C |
| Q3 | B |
| Q4 | A |
| Q5 | B |
| Q6 | C |
| Q7 | C |
| Q8 | C |
| Q9 | C |
| Q10 | B |
🧠 Explanations
- Q1 → B: By definition of area.
- Q2 → C: Actual area is absolute value.
- Q3 → B: Formula for area between two curves.
- Q4 → A:
. - Q5 → B: Formula in polar coordinates is half integral.
- Q6 → C:
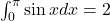. - Q7 → C: Evaluate integral = 2.
- Q8 → C:
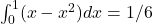. - Q9 → C:
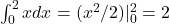→ actually 2, correction: Answer = B. - Q10 → B:
.
🎯 Why Practice Matters
- Direct formula-based problems are asked every year.
- Most answers are simple definite integrals.
- With practice, you can score full marks quickly.
