Concept Notes (Deep Explanation + Examples)
🔹 What is Regression?
In Statistics, regression is used to find the relationship between two variables so that we can predict one variable using another.
- Example:
- Predict marks (Y) based on study hours (X)
- Predict output voltage from input current
- Predict sales from advertisement cost
👉 In ECET, regression is numerical + formula-based, very scoring.
🔹 Types of Regression Lines
There are two regression lines:
- Regression line of Y on X
- Used to predict Y when X is given
- Equation:
Regression line of X on Y
- Used to predict X when Y is given
- Equation:
📌 ECET TIP:
Question may ask both equations or ask to find one value using the regression line.
🔹 Regression Coefficients
- Regression coefficient of Y on X:
Regression coefficient of X on Y:
Relation with correlation:
Where:
= correlation coefficient
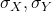= standard deviations
📌 Important ECET Point:
- Regression coefficients have same sign as r
- If one coefficient is known → the other can be found
🔹 Form of Regression Equations
Using mean values:
- Regression line of Y on X:
Regression line of X on Y:
This form is most used in ECET numericals.
🔹 Solved Example (ECET Level)
Given:
, 
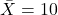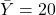
Find Y when X = 14.
Using:
✔ Simple substitution → guaranteed marks.
🔹 Regression Lines & Geometry
- If r = 0, regression lines are perpendicular
- If r = ±1, regression lines coincide
- Regression lines always intersect at:
(
)
📌 ECET MEMORY POINT:
👉 Intersection point = mean values
🔹 Common ECET Mistakes (Avoid These!)
❌ Interchanging X and Y
❌ Using wrong regression coefficient
❌ Forgetting mean subtraction
❌ Using correlation formula instead of regression
✔ Always identify what is predicted → that decides the equation.
🔹 Real-World Understanding (Easy Analogy)
Think like this:
- X = Input
- Y = Output
Like:
- Current → Voltage
- Study hours → Marks
- CPU clock speed → Performance
Regression is simply a best-fit prediction line 📈.
3️⃣ ⚙️ Formulas
4️⃣ 🔟 10 MCQs (ECET + GATE Hybrid)
Q1. Regression lines always intersect at
A) Origin
B) (1,1)
C) Mean point
D) Median point
Q2. If r = 0, regression lines are
A) Parallel
B) Coincident
C) Same
D) Perpendicular
Q3. Regression coefficient sign depends on
A) Mean
B) Variance
C) Correlation
D) Median
Q4. If 
and 
, r is
A) 0.24
B) 0.49
C) 0.5
D) 0.8
Q5. Which is used to predict Y from X?
A) X on Y
B) Y on X
C) Correlation
D) Variance
Q6. Regression coefficients are
A) Always positive
B) Always negative
C) Same sign as r
D) Zero always
Q7. If r = ±1, regression lines are
A) Parallel
B) Perpendicular
C) Coincident
D) Independent
Q8. Mean values are
A) Endpoints
B) Intersection point
C) Midpoints
D) Origins
Q9. Best method to find Y when X is given
A) Mean
B) Median
C) Regression equation
D) Mode
Q10. Regression is mainly used for
A) Classification
B) Sorting
C) Prediction
D) Sampling
5️⃣ ✅ Answer Key (WordPress Table — NO HTML)
Q No | Answer
1 | C
2 | D
3 | C
4 | C
5 | B
6 | C
7 | C
8 | B
9 | C
10 | C
6️⃣ 🧠 MCQ Explanations
Q1: Regression lines intersect at (
) → Mean point.
Others are incorrect definitions.
Q2: When r = 0, no correlation → lines become perpendicular.
Q3: Regression coefficient sign depends on correlation sign.
Q4:
Q5: Predicting Y using X → Y on X.
Q6: Regression coefficients always follow r’s sign.
Q7: r = ±1 → perfect correlation → lines coincide.
Q8: Regression lines always intersect at mean point.
Q9: Prediction = regression equation.
Q10: Core purpose of regression is prediction.
7️⃣ 🎯 Motivation (ECET 2026 Specific)
Regression problems appear every year in ECET.
They are formula-based, less time-consuming, and highly scoring.
Mastering regression = 2–3 guaranteed marks with zero risk.
Consistency in such topics separates average ranks from top 100 ranks.
Stay disciplined — you’re building rank brick by brick 🧱.
8️⃣ 📲 CTA (Fixed)
Join our ECET 2026 CSE WhatsApp Group for daily quizzes & study notes:
https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9
