Concept Notes

Applications of Derivatives – Maxima & Minima

1. Derivative →
   The derivative of a function tells us the rate of change.

• If 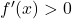→ function is increasing.
• If 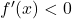→ function is decreasing.

2. Critical Points →

• Points where or → Local Minimum.
• If 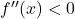→ Local Maximum.
• If 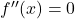→ Test fails (use higher derivatives or graph).

---

⚙️ Important Formulas

• First Derivative Test:
  If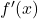 changes sign from +ve to -ve at , then Maxima.
  If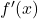 changes sign from -ve to +ve at , then Minima.
• Second Derivative Test:
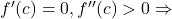  Local Minima.
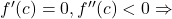  Local Maxima.
• Example function:
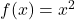  → Minima at .
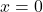  → Maxima at .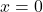

---

✨ Examples

1. 

• 
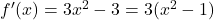
• Critical points →
• 
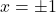
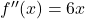
  • At 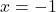, 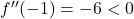→ Maxima.
  • At 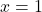, 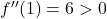→ Minima.

---

🔟 10 MCQs

Q1. If , then at the function has:
(A) Maxima (B) Minima (C) Saddle point (D) None

Q2. has maxima at:
(A) 0 (B) 1 (C) -1 (D) None

Q3. For , the point is:
(A) Maxima (B) Minima (C) Neither (D) Both

Q4. If and , then is:
(A) Maxima (B) Minima (C) Inflection (D) Undefined

Q5. For , minima occurs at:
(A) 0 (B) 1 (C) -1 (D) None

Q6. If , then maxima is at:
(A) 0 (B) -1 (C) 1 (D) 2

Q7. For , maxima occurs at:
(A) 0 (B) (C) (D)

Q8. has minima at:
(A) 0 (B) (C) (D)

Q9. If , then extrema is at:
(A) 0 (B) 1 (C) -1 (D) None

Q10. Second derivative test is used for:
(A) Increasing function (B) Max/Min test (C) Continuity (D) Limits

---

✅ Answer Key

Q.No	Answer
1	B
2	A
3	C
4	B
5	A
6	B
7	B
8	C
9	D
10	B

---

🧠 Explanations

• Q1: 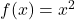, → Minima.
• Q2: , 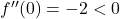→ Maxima at 0.
• Q3: 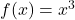, 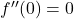→ neither Max nor Min.
• Q4: Second derivative test says 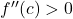→ Minima.
• Q5: , minima at 0.
• Q6: Done in example, maxima at -1.
• Q7: 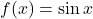, maxima at .
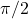• Q8: 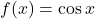, minima at .
• Q9: 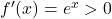, no extrema.
• Q10: By definition.

---

🎯 Motivation / Why Practice Matters

Applications of derivatives are key in solving optimization problems (max profit, min cost, max area, min time, etc).
By practicing maxima & minima, you’ll build confidence for real-life engineering and ECET exam problems.

---

📲 CTA

👉 Want more practice? Join our study group here: Join ECET Group