Concept Notes – Asymptotic Notation
🌐 What is Asymptotic Notation?
- Used to describe the efficiency of algorithms.
- Focuses on growth rate of functions as input size n→∞n \to \inftyn→∞.
- Helps compare algorithms regardless of hardware or constants.
🏷️ Types of Asymptotic Notation
- Big O (O) – Upper Bound
- Defines worst-case complexity.
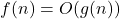 means f(n) grows at most as fast as g(n).
means f(n) grows at most as fast as g(n).
- Big Omega (Ω) – Lower Bound
- Defines best-case complexity.
 means f(n) grows at least as fast as g(n).
means f(n) grows at least as fast as g(n).
- Big Theta (Θ) – Tight Bound
- Defines exact growth (both upper and lower).
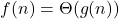 means f(n) grows exactly as g(n).
means f(n) grows exactly as g(n).
📚 Examples
- Linear search in array of size n:
- Best case → first element →
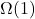
- Worst case → last element →
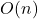
- Average case →
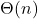
- Best case → first element →
- Binary search in sorted array of size n:
- Best case → middle element →
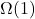
- Worst case → logarithmic splits →
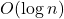
- Average case →

- Best case → middle element →
⚙️ Formulas
- Big O definition:
![]()
Big Omega definition:
![]()
Big Theta definition:
![]()
Common growth functions: ![]()
🔟 10 MCQs – GATE 2026 Algorithms
Q1. If f(n) = 5n^2 + 3n + 2, the Big O notation is:
A) O(n)
B) O(n^2)
C) O(n^3)
D) O(log n)
Q2. If f(n) = 2n + 7, then Big Ω notation is:
A) Ω(1)
B) Ω(n)
C) Ω(n^2)
D) Ω(log n)
Q3. Binary search worst-case complexity is:
A) O(n)
B) O(log n)
C) O(n log n)
D) O(1)
Q4. Big Θ notation defines:
A) Upper bound
B) Lower bound
C) Exact bound
D) None of these
Q5. Linear search best case complexity:
A) Θ(n)
B) Ω(1)
C) O(n^2)
D) Θ(log n)
Q6. Which of the following functions grows fastest?
A) n^2
B) n log n
C) 2^n
D) n
Q7. f(n) = 3n^3 + 4n^2 + n. Then Θ(f(n)) = ?
A) Θ(n^2)
B) Θ(n^3)
C) Θ(n^4)
D) Θ(n log n)
Q8. Which of the following statements is correct?
A) O(g(n)) = Θ(g(n)) always
B) Θ(g(n)) ⊆ O(g(n))
C) Ω(g(n)) = O(g(n))
D) Θ(g(n)) ⊆ Ω(g(n))
Q9. If f(n) = log n + 100, O(f(n)) is:
A) O(1)
B) O(n)
C) O(log n)
D) O(n log n)
Q10. Which of the following represents a tight bound?
A) O(n^2) for f(n) = n^2 + 3n
B) Ω(n^2) for f(n) = n^2 + 3n
C) O(n^3) for f(n) = n^2 + 3n
D) Ω(n) for f(n) = n^2 + 3n
✅ Answer Key
| Q.No | Answer |
|---|---|
| 1 | B |
| 2 | B |
| 3 | B |
| 4 | C |
| 5 | B |
| 6 | C |
| 7 | B |
| 8 | B |
| 9 | C |
| 10 | A |
🧠 Explanations
- Leading term 5n^2 → O(n^2)
- 2n dominates for large n → Ω(n)
- Binary search halves array each step → O(log n)
- Θ = both upper and lower bounds → exact growth
- Linear search best case → first element → Ω(1)
- Exponential 2^n grows faster than polynomial/logarithmic functions
- Leading term 3n^3 → Θ(n^3)
- Θ(g(n)) ⊆ O(g(n)) and Θ(g(n)) ⊆ Ω(g(n))
- Constant 100 negligible → O(log n)
- n^2 + 3n grows exactly as n^2 → tight bound → O(n^2)
🎯 Motivation / Why Practice Matters
- Asymptotic notation is fundamental for analyzing algorithms.
- Almost every GATE Algorithms question requires time/space complexity analysis.
- Mastery here helps in coding interviews and competitive programming.
- Clear understanding helps choose the most efficient solution under constraints.
📲 CTA
Join our GATE 2026 CSE Algorithms Prep Community: @LearnNewThingsHub