
Concept Notes (Deep Explanation + Examples)
🔹 Introduction
In real-life civil engineering structures, members are rarely subjected to just one type of load.
A beam might bend under load (bending stress), twist slightly (torsional stress), or get compressed at one end and tensioned at the other.
When two or more stresses act on a body simultaneously, it is said to be under Combined Stress.
Combined stresses are extremely important in bridge piers, beam-columns, shafts, and dam walls.
🔹 Types of Combined Stresses
- Axial + Bending Stress
When a column carries both direct load and bending moment.
Example: A streetlight pole fixed at the base and subjected to wind pressure → tension on one side, compression on the other. - Axial + Torsional Stress
Seen in shafts carrying both torque and axial load.
Example: A transmission shaft in a construction mixer. - Bending + Shear Stress
Occurs in beams where both bending and shear act simultaneously. - Bi-axial Stress
Occurs when normal stresses act in two perpendicular directions (x and y).
Example: Thin-walled pressure vessels (cylindrical tanks). - Combined Normal and Shear Stress
Common in structures where external loads produce both shear and normal stresses.
🔹 Principal Planes and Principal Stresses
When a member is subjected to combined normal and shear stresses, there exist planes where the shear stress is zero, and only normal stress acts.
These planes are called Principal Planes, and the stresses on them are Principal Stresses.
🔹 Formula Derivation (Concept)
Let a point be subjected to:
- Normal stress in x-direction:

- Normal stress in y-direction:
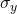
- Shear stress:

Then, the Principal Stresses are given by:
![]()
The Maximum Shear Stress is:
![]()
🔹 Mohr’s Circle (Concept Visualization)
To visualize combined stress, Mohr’s Circle is used.
It is a graphical method to find:
- Principal stresses
- Principal planes
- Maximum shear stress
🌀 Imagine plotting normal stress (x-axis) and shear stress (y-axis).
The circle’s center and radius give the mean stress and maximum shear stress respectively.
🔹 Real-World Civil Example
- Bridge Pier under Water Flow:
Vertical load (axial) due to structure weight + horizontal force (bending) due to water pressure → combined stress. - Crane Hook:
Experiences bending, shear, and tensile stresses together. - Dam Section:
Weight of water exerts horizontal stress; dam weight causes vertical stress → combined normal stresses.
🔹 Field Tip
When checking safety of a member, the maximum principal stress or maximum shear stress should always be within permissible limits as per material yield strength.
3️⃣ ⚙️ Formulas (Plain LaTeX Only — No Boxes)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4️⃣ 🔟 10 MCQs (GATE + ECET Mix)
- When two perpendicular normal stresses and one shear stress act on a plane, the condition is known as:
A) Uniaxial stress
B) Simple shear
C) Combined stress
D) Torsional stress - Principal stresses occur on planes where:
A) Shear stress is maximum
B) Shear stress is zero
C) Normal stress is zero
D) Both are equal - The equation for principal stress is derived using:
A) Hooke’s Law
B) Mohr’s Circle
C) Bernoulli’s theorem
D) Euler’s formula - If
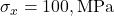 ,
, 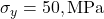 , and
, and 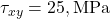 , then
, then  = ?
= ?
A) 25 MPa
B) 27.95 MPa
C) 35.35 MPa
D) 45.45 MPa - In Mohr’s Circle, the x-axis represents:
A) Shear stress
B) Normal stress
C) Strain
D) Principal plane angle - Combined bending and axial load occurs in:
A) Simply supported beam
B) Column with eccentric load
C) Fixed beam
D) Cantilever beam - The maximum shear stress acts at:
A) 0°
B) 45°
C) 90°
D) 180° - The stress due to bending is proportional to:
A) Area
B) Moment of inertia
C) Distance from neutral axis
D) Radius of curvature - The relation between principal stresses in a thin cylinder is:
A)
B)
C)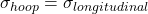
D) None - When
 and
and 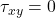 , the state of stress is:
, the state of stress is:
A) Pure shear
B) Hydrostatic
C) Simple tension
D) Principal
5️⃣ ✅ Answer Key (WordPress Table Format — NO HTML)
Q.No Answer
1 C
2 B
3 B
4 B
5 B
6 B
7 B
8 C
9 A
10 B
6️⃣ 🧠 Explanations (Step-by-Step)
1️⃣ Combined stress occurs when more than one stress acts → ✅ C
2️⃣ Principal planes have zero shear stress → ✅ B
3️⃣ Formula derived graphically using Mohr’s circle → ✅ B
4️⃣ ![]() → ✅ B
→ ✅ B
5️⃣ X-axis is for normal stress, Y-axis for shear → ✅ B
6️⃣ Column with eccentric load → bending + axial → ✅ B
7️⃣ Max shear acts at 45° → ✅ B
8️⃣ ![]() → ✅ C
→ ✅ C
9️⃣ In thin cylinders, hoop = 2 × longitudinal → ✅ A
10️⃣ Equal normal stresses with zero shear = hydrostatic → ✅ B
7️⃣ 🎯 Motivation / Why Practice Matters (ECET 2026 Civil)
Combined Stress questions appear every year in ECET and GATE because they test concept clarity + formula application.
If you can visualize how stresses combine and calculate principal stresses, you can easily handle advanced RCC and structural design topics later.
👉 Remember, concept clarity > memorization.
Once you grasp how forces interact inside materials, Civil Engineering becomes logical and enjoyable.
Keep practicing — every problem you solve adds confidence for ECET 2026!
8️⃣ 📲 CTA
Join our ECET 2026 Civil WhatsApp Group for daily quizzes & study notes:
🔗 https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9



