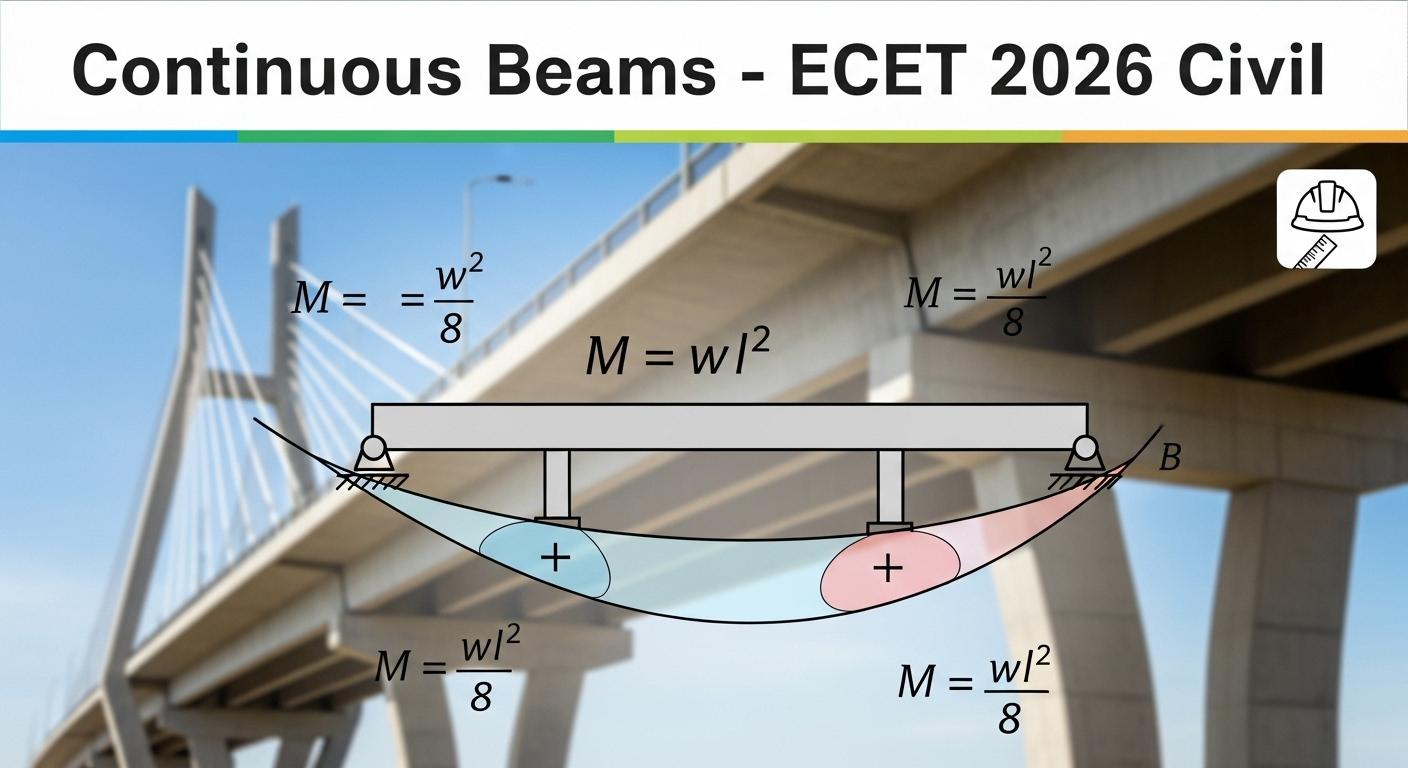
Why this topic is important for ECET
Continuous beams are a high-weightage area in Theory of Structures because they test your ability to handle redundant supports, bending moment distribution, and shear force analysis. ECET regularly includes numerical problems on three-moment equation, Clapeyron’s theorem, and support settlements. If you master this, you’ll save time and secure easy marks.
📘 Concept Notes
1. What is a Continuous Beam?
- A continuous beam is one which is supported on more than two supports.
- Unlike simply supported beams, continuous beams are statically indeterminate.
- Common in bridges, multi-span structures, and floor systems.
2. Advantages of Continuous Beams
- Reduced maximum bending moment compared to simply supported beams.
- Economy in material usage.
- Better structural stability and serviceability.
3. Analysis Methods for Continuous Beams
(a) Clapeyron’s Theorem of Three Moments
For three consecutive supports A, B, C with spans AB = l₁ and BC = l₂:
where:
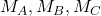= moments at supports,
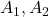= areas of bending moment diagrams for spans AB, BC,
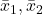= distances of centroid of BM diagrams from supports.
(b) Moment Distribution Method
- Successive distribution of moments to supports until balance is achieved.
- Useful for hand calculations when indeterminacy is small.
(c) Slope Deflection Method
- Based on relation between moments, rotations, and displacements.
- More theoretical, but helps understand stiffness concept.
4. Example
Problem: A continuous beam ABC with equal spans of 6 m each carries a uniform load of 10 kN/m on both spans. Ends are simply supported.
Solution using Three-Moment Theorem:
- Spans:
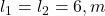. - BM area for UDL span =
. - Centroid from support =
.
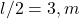Equation:
Hence, negative BM at middle support.
⚙️ Formulas
🔟 10 MCQs
Q1. A continuous beam is defined as:
a) Beam with two supports
b) Beam with more than two supports
c) Beam with one end fixed
d) Beam without supports
Q2. Continuous beams are:
a) Statically determinate
b) Statically indeterminate
c) Both
d) None
Q3. The three-moment equation is used to calculate:
a) Deflection only
b) Shear force only
c) Support moments
d) Reactions directly
Q4. In Clapeyron’s theorem, the term 
represents:
a) Span length
b) Area of BM diagram × distance of centroid
c) Shear force
d) Load intensity
Q5. Maximum bending moment in a simply supported beam with UDL 
over span 
:
a) 
b) 
c) 
d) 
Q6. A two-span continuous beam of equal spans with UDL will have:
a) Positive BM at supports
b) Negative BM at intermediate support
c) Zero BM everywhere
d) None
Q7. Moment distribution method is based on:
a) Area theorem
b) Distribution of fixed-end moments
c) Shear equations
d) Poisson’s ratio
Q8. A 6 m span continuous beam with 20 kN/m UDL has fixed-end moment:
a)
b)
c)
d) 
Q9. Continuous beams are economical because:
a) They reduce max BM
b) They reduce span length
c) They reduce material cost
d) None
Q10. Deflection under UDL in a simply supported beam is:
a) 
b) 
c) 
d) 
✅ Answer Key
| Q | Answer |
|---|---|
| 1 | b |
| 2 | b |
| 3 | c |
| 4 | b |
| 5 | b |
| 6 | b |
| 7 | b |
| 8 | b |
| 9 | a |
| 10 | b |
🧠 Explanations
- Q1: Continuous beam → more than two supports → (b).
- Q2: Extra supports make system indeterminate → (b).
- Q3: Three-moment theorem → gives support moments → (c).
- Q4: In theorem, 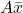= area of BM diagram × centroid → (b).
- Q5: Max BM under UDL = 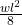→ (b).
- Q6: Negative BM develops at middle support → (b).
- Q7: Moment distribution method balances fixed-end moments → (b).
- Q8: Fixed-end moment for UDL = 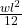→ (b).
- Q9: Economical because max BM reduces → (a).
- Q10: Deflection under UDL = → (b).
🎯 Motivation / Why Practice Matters
In ECET 2026, continuous beams questions are often numerical and appear in 3–5 marks range. These problems are formula-driven, so if you know the three-moment equation and moment distribution basics, you can solve them in under a minute.
👉 Practicing ensures you won’t waste time in the exam, giving you an edge over others.
📲 CTA
Join our WHATSAPP group for ECET 2026 updates and discussions →
👉 https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9
