Concept Notes (Deep Explanation + Examples)
A definite integral represents the area under a curve between two limits.
Unlike indefinite integrals (which give a family of functions + constant ![]() ), definite integrals give a numerical value.
), definite integrals give a numerical value.
🔹 BASIC DEFINITION
If ![]() is continuous on
is continuous on ![]() ,
,
then the definite integral of ![]() from
from ![]() to
to ![]() is:
is:
![]()
where ![]() .
.
That is, integrate first, then substitute limits.
🔹 GEOMETRICAL MEANING
It represents the net area under the curve ![]() from
from ![]() to
to ![]() .
.
- Area above x-axis → positive
- Area below x-axis → negative
🧮 Example:
Find ![]()
→ ![]()
✅ So, area = ![]() square units.
square units.
⚡ PROPERTIES OF DEFINITE INTEGRALS
These properties help simplify long integrals quickly (important for ECET & GATE):
1️⃣ Property of Limits Exchange
![]()
Swapping limits changes the sign of the integral.
2️⃣ Property of Zero Interval
![]()
If both limits are same → area = 0.
3️⃣ Sum Property
![]()
Integrals distribute over addition/subtraction.
4️⃣ Property of Constant Multiplication
![]()
5️⃣ Property of Splitting Interval
![]()
This helps when a function changes its behavior at point ![]() .
.
6️⃣ Property of Symmetry (Even-Odd)
For symmetric limits ![]() to
to ![]() :
:
- If
 is even,
is even,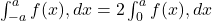
Example:
- If
 is odd,
is odd,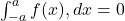
Example: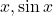
7️⃣ Property of Substitution
If ![]() , then
, then
![]()
This is a very useful shortcut for many ECET problems.
🧮 Example:
Find ![]()
By property, ![]() .
.
No change → evaluate directly:
![]()
8️⃣ Average Value of Function
Average value of ![]() in
in ![]() is:
is:
![]()
🧠 ECET Level Example:
Find ![]()
= ![]()
= ![]() .
.
✅ Final Answer = ![]()
🧩 Real-World Connection
- In Physics, it’s used for work done by a variable force.
- In Computer Graphics, used for area and shading calculations.
- In Data Science, integrals help in finding probability density areas under curves.
⚙️ Formulas
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
🔟 10 MCQs (ECET + GATE Hybrid)
- The value of
 is
is
A) 2 B) 8 C) 4/3 D) 8/3 - If
 , then
, then 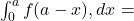 ?
?
A) -5 B) 5 C) 10 D) 0  equals
equals
A) 0 B) 1 C) 2 D) -2 = ?
= ?
A) 0 B) 1 C) 1/2 D) -1/2- The integral
 equals
equals
A) 0 B) 2∫ₐᵇf(x)dx C) ∫ₐᵇf(x)dx D) -∫ₐᵇf(x)dx  = ?
= ?
A) 0 B) 4 C) 8 D) -8 = ?
= ?
A) 1 B) 2 C) -1 D) 0- If
 is even, then
is even, then  ?
?
A) 0 B) ∫₀ᵃf(x)dx C) 2∫₀ᵃf(x)dx D) -2∫₀ᵃf(x)dx 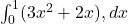 = ?
= ?
A) 1 B) 2 C) 3 D) 4- The average value of
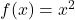 on
on ![Rendered by QuickLaTeX.com [0,2]](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-1571666a47302be9ed925a760be14ff0_l3.png) is
is
A) 4/3 B) 2 C) 8/3 D) 1
✅ Answer Key
Q No | Answer
1 | D
2 | B
3 | C
4 | C
5 | A
6 | A
7 | D
8 | C
9 | B
10 | A
🧠 MCQ Explanations
1️⃣ ![]()
2️⃣ ![]()
3️⃣ ![]()
4️⃣ ![]()
5️⃣ Property: ![]()
6️⃣ Odd function over symmetric limits → 0 → A
7️⃣ ![]()
8️⃣ Even function → ![]()
9️⃣ ![]()
10️⃣ latex∫_0^2x^2dx=(1/2)*(8/3)=4/3→A[/latex]
🎯 Motivation (ECET 2026 Specific)
Definite Integrals repeat every single year in ECET — both conceptual and numerical forms.
It tests your accuracy, concept clarity, and speed.
Mastering properties like symmetry and substitution can boost your score by 5–8 marks instantly.
Practice daily, visualize the curve, and never skip basic property-based questions — they’re rank boosters!
📲 CTA (Fixed)
Join our ECET 2026 CSE WhatsApp Group for daily quizzes & study notes:
👉 https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9