Differentiation is one of the most important topics in Engineering Mathematics. ECET 2026 students can expect 2–3 direct questions from this chapter. If you master the basic derivative rules, you can solve even complex calculus problems easily.
📘 Concept Notes – Differentiation
👉 Definition:
Differentiation is the process of finding the derivative of a function.
The derivative of a function measures the rate of change of the function with respect to its variable.
- If y=f(x)y = f(x)y=f(x), then derivative is written as:
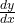or 
.
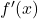⚙️ Basic Derivative Rules
- Power Rule:
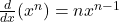
Example: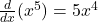
- Constant Rule:
Example: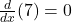
- Constant × Function Rule:
![\frac{d}{dx}[c \cdot f(x)] = c \cdot f'(x)](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-5a5be5c6468e2f64def62a41290dceb3_l3.png "Rendered by QuickLaTeX.com")
Example:![\frac{d}{dx}[4x^3] = 12x^2](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-4f9d75300341c9fc58640784ebaab1d3_l3.png "Rendered by QuickLaTeX.com")
- Sum Rule:
![\frac{d}{dx}[f(x) + g(x)] = f'(x) + g'(x)](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-1d5f3777a9bd7ac0697156afe234ddfd_l3.png "Rendered by QuickLaTeX.com")
Difference Rule:
![\frac{d}{dx}[f(x) - g(x)] = f'(x) - g'(x)](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-51c5e43b0f816950ce659e53454af448_l3.png "Rendered by QuickLaTeX.com")
Exponential Function:![\frac{d}{dx}[e^x] = e^x](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-c3bad4eecb2508ccf7186be71a465440_l3.png "Rendered by QuickLaTeX.com")
![\frac{d}{dx}[a^x] = a^x \ln a](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-94849ec28407e672c44259c16fdcd450_l3.png "Rendered by QuickLaTeX.com")
Logarithmic Function:
![\frac{d}{dx}[\ln x] = \frac{1}{x}](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-f485f32e06de7a5316d740f51da3c483_l3.png "Rendered by QuickLaTeX.com")
Trigonometric Functions:
✍️ Example Problems
Example 1:
Find derivative of 
.
Solution:
Example 2:
Find derivative of 
.
Solution:
Example 3:
Find derivative of 
.
Solution:
🔟 10 Most Expected MCQs – ECET 2026
Q1. Derivative of 
is:
A) 
B) 
C)
D) 
Q2. Derivative of a constant is:
A) 1
B) 0
C) Infinity
D) Same constant
Q3. 
= ?
A) 
B) 
C) 
D) None
Q4. Derivative of is:
A) x
B) 
C) 
D)
Q5. 
= ?
A) 
B) 
C) 
D) 
Q6. 
= ?
A) 
B)
C)
D) 
Q7. 
= ?
A) 
B)
C) 
D) 
Q8. 
= ?
A) 
B) 
C)
D) 
Q9. 
= ?
A) 
B) 
C) 
D) 
Q10. Derivative of 
is:
A) 
B)
C) 
D) 
✅ Answer Key (Table)
| Q.No | Answer |
|---|---|
| Q1 | B |
| Q2 | B |
| Q3 | A |
| Q4 | B |
| Q5 | A |
| Q6 | B |
| Q7 | B |
| Q8 | B |
| Q9 | A |
| Q10 | A |
🧠 Explanations of Answers
- Q1 → B: Power rule →
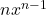, so derivative of 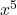= . - Q2 → B: Derivative of any constant is 0.
- Q3 → A: Derivative of 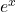is .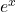
- Q4 → B:
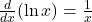. - Q5 → A: Derivative of 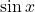is .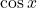
- Q6 → B: Derivative of 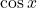is .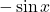
- Q7 → B: Derivative of is .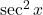
- Q8 → B: Derivative of 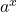is .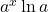
- Q9 → A: Derivative of = .
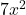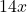- Q10 → A: Derivative of = .
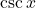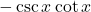🎯 Why This Practice Matters for ECET 2026
Differentiation is a core part of Calculus. In ECET exams, questions are mostly direct formula-based, making them scoring topics. By memorizing and practicing basic derivatives, you can solve integration, maxima-minima, and applied problems faster.
📲 Join Our ECET Prep Community on Telegram
Want daily ECET MCQs, solved problems, and video sessions?
👉 Join here: @LearnNewThingsHub
