Concept Notes (Deep Explanation + Examples)
🔹 Introduction
In Civil Engineering, columns and struts are compression members designed to carry axial loads.
- A column is a vertical compression member (e.g., pillars in buildings).
- A strut is a compression member that may be inclined or horizontal, often used in trusses or bridge structures.
When these members are subjected to axial compressive loads, they tend to buckle (bend sideways) if the load exceeds a certain limit. Understanding this buckling behavior is vital for safe design.
🔹 Types of Columns
- Based on Length:
- Short Column: Fails by crushing (no buckling).
Long Column: Fails by buckling.
Intermediate Column: Fails by both crushing and buckling.
Based on End Conditions:
- Both ends hinged
- Both ends fixed
- One end fixed, other free
- One end fixed, other hinged
🔹 Euler’s Column Theory (Long Columns)
Euler’s theory applies to long, slender columns made of elastic materials, where failure occurs by buckling rather than crushing.
The critical load (also called buckling load) is the axial load at which a column just begins to buckle.
Euler’s Formula:
Where:
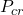= Critical load
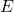= Young’s modulus
= Moment of inertia
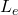= Effective length depending on end conditions
🔹 Effective Length for Different End Conditions
| End Conditions | Effective Length (Le) | Remarks |
|---|---|---|
| Both ends hinged |  | Buckles in one half wave |
| Both ends fixed |  | Strongest column |
| One end fixed, other free |  | Weakest column |
| One end fixed, other hinged |  | Intermediate strength |
🔹 Example (Field Scenario)
Suppose we have a steel column (E = 2×10⁵ N/mm²),
I = 8×10⁶ mm⁴,
L = 3 m,
both ends hinged.
Then,
So, the column will buckle if the load exceeds 17.55 kN.
🔹 Rankine’s Formula (Intermediate Columns)
For intermediate-length columns, both crushing and buckling act together.
The Rankine formula combines Euler’s and crushing effects.
Or
Where:
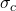= Crushing stress
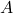= Cross-sectional area
= Rankine constant (depends on material)
= Radius of gyration
Typical values of ‘a’:
| Material | a value |
|---|---|
| Mild Steel | 1/7500 |
| Cast Iron | 1/1600 |
| Timber | 1/1000 |
🔹 Example (Numerical)
A mild steel column (A = 6000 mm², 
, 
)
Using Rankine:
🔹 Field Application
In construction sites:
- Short columns: in ground floors or heavy foundations.
- Long columns: in multi-story buildings, towers, bridges.
- Struts: used in truss roofs, bridge frameworks, scaffolding.
🔹 Exam Tips
- Euler → Long columns
- Rankine → Intermediate columns
- Crushing → Short columns
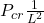
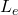- depends on end conditions (frequently asked in ECET & GATE).
⚙️ Formulas (Plain LaTeX Only)
🔟 10 MCQs (GATE + ECET Mix)
- Euler’s formula is valid for
A) Short columns
B) Long columns
C) Both
D) None - Effective length for both ends fixed column is
A) L
B) 2L
C) L/2
D) L/√2 - The weakest column condition is
A) Both ends fixed
B) One end fixed and other free
C) Both ends hinged
D) One end fixed and other hinged - Rankine’s constant for mild steel is approximately
A) 1/7500
B) 1/1600
C) 1/1000
D) 1/9000 - The crushing load is given by
A)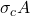
B)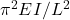
C)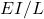
D) None - In Rankine’s formula, if
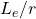→ 0, then
A)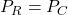
B)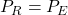
C)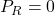
D) None - The ratio
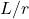is called
A) Effective ratio
B) Slenderness ratio
C) Flexural ratio
D) Column ratio - Euler’s load varies
A) Directly with L
B) Inversely with L
C) Inversely with L²
D) Directly with L² - Rankine’s formula combines
A) Bending and torsion
B) Crushing and buckling
C) Shear and compression
D) Tension and torsion - In a column with both ends hinged, the first buckling shape is
A) One-half sine wave
B) One full sine wave
C) Straight
D) None
✅ Answer Key
Q.No Answer
1 B
2 C
3 B
4 A
5 A
6 A
7 B
8 C
9 B
10 A
🧠 Explanations (Step-by-Step)
1️⃣ (B) Euler’s formula applies to long slender columns that fail by buckling.
2️⃣ (C) For both ends fixed, 
.
3️⃣ (B) One end fixed and other free is weakest because effective length = 2L.
4️⃣ (A) For mild steel, Rankine’s constant a = 1/7500.
5️⃣ (A) Crushing load = .
6️⃣ (A) For 
, denominator = 1 ⇒ .
7️⃣ (B) defines the slenderness of a column.
8️⃣ (C) 
(inversely proportional to L²).
9️⃣ (B) Rankine formula combines crushing + buckling.
10️⃣ (A) For both ends hinged, the buckling mode is half-sine wave.
🎯 Motivation / Why Practice Matters (ECET 2026 Civil)
Columns are one of the most frequent ECET topics because they connect theory and field practice — from understanding slenderness to designing reinforced columns.
Practicing Euler and Rankine problems builds your ability to solve tricky design questions fast, giving you an edge in competitive exams.
Stay consistent — civil engineering becomes easy when you understand how loads actually behave on site.
Every day of practice brings you closer to your ECET dream rank. 🚀
📲 CTA
Join our ECET 2026 Civil WhatsApp Group for daily quizzes & study notes:
👉 https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9
