
Concept Notes
1. What is Modulation?
- Modulation is the process of varying a carrier wave parameter (amplitude, frequency, or phase) according to the message signal.
- In PM (Phase Modulation), the phase of carrier is varied proportional to the instantaneous amplitude of the modulating signal.
2. Phase Modulation (PM) Definition
- The instantaneous phase of carrier signal is varied linearly with the modulating signal.
Carrier signal:
![]()
PM signal:
![]()
Where,
 = carrier amplitude
= carrier amplitude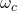 = carrier angular frequency
= carrier angular frequency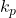 = phase sensitivity (radians/volt)
= phase sensitivity (radians/volt)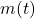 = message signal
= message signal
3. Phase Deviation
- The maximum change in phase due to modulation is phase deviation.
![]()
Where ![]() = peak amplitude of message signal.
= peak amplitude of message signal.
4. Bandwidth of PM Signal
Using Carson’s Rule:
![]()
But in PM, frequency deviation depends on modulating frequency:
![]()
So, bandwidth of PM is generally larger than FM for high frequencies.
5. Relation between PM & FM
- Both are angle modulation techniques.
- FM: frequency varies with message signal.
- PM: phase varies with message signal.
Conversion:
- PM can be obtained from FM by integrating the message signal.
- FM can be obtained from PM by differentiating the message signal.
⚙️ Important Formulas
PM Signal:
![]()
Phase Deviation:
![]()
Instantaneous Phase:
![]()
Instantaneous Frequency (PM):
![]()
Carson’s Rule (approximate bandwidth):
![]()
🔢 Example
If ![]() , message signal
, message signal ![]() .
.
- Maximum phase deviation:
![]()
Bandwidth (Carson’s Rule):
Message frequency ![]() .
.
![]()
So, ![]()
🔟 10 MCQs
Q1. In PM, which parameter of carrier is varied?
a) Amplitude
b) Frequency
c) Phase
d) Both amplitude & phase
Q2. The equation of a PM signal is:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Q3. The phase deviation in PM is given by:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Q4. PM is classified as:
a) Amplitude modulation
b) Angle modulation
c) Pulse modulation
d) None
Q5. Carson’s Rule gives:
a) Power of signal
b) Bandwidth of signal
c) Phase deviation
d) Noise performance
Q6. PM and FM belong to:
a) Analog modulation
b) Digital modulation
c) Both
d) None
Q7. In PM, instantaneous frequency depends on:
a) Amplitude of m(t)
b) Derivative of m(t)
c) Integral of m(t)
d) Constant
Q8. PM can be derived from FM by:
a) Differentiation of m(t)
b) Integration of m(t)
c) Using AM techniques
d) None
Q9. If ![]() and
and ![]() , then phase deviation is:
, then phase deviation is:
a) 1 rad
b) 5 rad
c) 10 rad
d) 100 rad
Q10. The bandwidth of PM signal is generally:
a) Smaller than FM
b) Equal to FM
c) Larger than FM
d) Zero
✅ Answer Key
| Q No | Answer |
|---|---|
| Q1 | c |
| Q2 | c |
| Q3 | a |
| Q4 | b |
| Q5 | b |
| Q6 | a |
| Q7 | b |
| Q8 | a |
| Q9 | c |
| Q10 | c |
🧠 Explanations
- Q1: PM → carrier phase varies.
- Q2: PM signal equation =
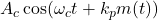 .
. - Q3: Phase deviation =
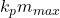 .
. - Q4: PM is angle modulation.
- Q5: Carson’s Rule estimates bandwidth.
- Q6: FM & PM are analog modulation techniques.
- Q7: Instantaneous frequency in PM depends on derivative of m(t).
- Q8: FM ↔ PM relation: differentiation/integration of message.
- Q9:
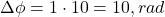 .
. - Q10: PM bandwidth > FM for high f.
🎯 Motivation
Phase Modulation is the backbone of digital communication (used in PSK, 4QAM, etc.).
If you master PM basics, ECET numericals on modulation index, bandwidth, and deviation become very easy.
👉 Remember: “Strong basics in PM = confidence in advanced modulation schemes.”
📲 CTA
👉 Want daily ECET quizzes & notes?
Join our WhatsApp group here:
🔗 Join Now



