
Concept Notes
1. Introduction to Logic Gates
- Logic gates are the building blocks of digital circuits.
- They perform Boolean algebra operations on binary inputs (0 or 1).
- Basic types: AND, OR, NOT.
- Universal gates: NAND, NOR.
- Other: XOR, XNOR.
2. Basic Gates
(a) AND Gate
- Output = 1 only if all inputs = 1.
- Boolean:

(b) OR Gate
- Output = 1 if any input = 1.
- Boolean:
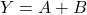
(c) NOT Gate
- Inverts input.
- Boolean:
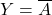
3. Universal Gates
(a) NAND Gate
- Equivalent to AND + NOT.
- Boolean:
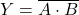
- Can implement any logic function.
(b) NOR Gate
- Equivalent to OR + NOT.
- Boolean:

- Also universal gate.
4. Other Gates
(a) XOR (Exclusive OR)
- Output = 1 if inputs are different.
- Boolean:

(b) XNOR (Exclusive NOR)
- Output = 1 if inputs are same.
- Boolean:
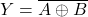
5. Truth Tables
| Gate | Expression | (A=0,B=0) | (A=0,B=1) | (A=1,B=0) | (A=1,B=1) |
|---|---|---|---|---|---|
| AND | 0 | 0 | 0 | 1 | |
| OR | 0 | 1 | 1 | 1 | |
| NOT | 1 (if A=0) | 0 (if A=1) | – | – | |
| NAND | 1 | 1 | 1 | 0 | |
| NOR | 1 | 0 | 0 | 0 | |
| XOR | 0 | 1 | 1 | 0 | |
| XNOR | 1 | 0 | 0 | 1 |
⚙️ Formulas
- AND:

- OR:
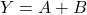
- NOT:
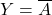
- NAND:
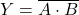
- NOR:

- XOR:

- XNOR:
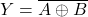
💡 Example
Q: Simplify using only NAND gates:
![]()
Ans:
- Step 1: OR =

- Step 2: Apply De Morgan →

- Step 3: Implement using NAND → NAND(NAND(A,A), NAND(B,B))
🔟 10 MCQs
Q1. The output of an AND gate is 1 when:
a) All inputs are 0
b) All inputs are 1
c) Any input is 1
d) Inputs are different
Q2. The Boolean expression for a NAND gate is:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Q3. The XOR gate output is 1 when:
a) Inputs are same
b) Inputs are different
c) All inputs are 0
d) All inputs are 1
Q4. Which gate is known as universal gate?
a) AND
b) OR
c) XOR
d) NAND
Q5. The Boolean expression ![]() represents:
represents:
a) XOR
b) NOR
c) NAND
d) XNOR
Q6. NOR gate output is 1 when:
a) Any input is 1
b) All inputs are 0
c) Inputs are different
d) All inputs are 1
Q7. Which gate is equivalent to the complement of OR?
a) NAND
b) NOR
c) XOR
d) XNOR
Q8. The output of an XNOR gate is 1 when:
a) Inputs are different
b) Inputs are same
c) First input is 1
d) Second input is 0
Q9. The minimum number of NAND gates required to implement an OR gate is:
a) 1
b) 2
c) 3
d) 4
Q10. If A=1 and B=0, the output of ![]() is:
is:
a) 0
b) 1
c) 2
d) Undefined
✅ Answer Key
| Q No | Answer |
|---|---|
| Q1 | b |
| Q2 | b |
| Q3 | b |
| Q4 | d |
| Q5 | a |
| Q6 | b |
| Q7 | b |
| Q8 | b |
| Q9 | c |
| Q10 | b |
🧠 Explanations
- Q1: AND → only when all inputs are 1 → (b).
- Q2: NAND = NOT(AND) =
 .
. - Q3: XOR = 1 when inputs differ.
- Q4: NAND & NOR are universal; here answer is NAND.
- Q5: Given = XOR form.
- Q6: NOR = NOT(OR); OR is 1 if any input =1 → so NOR is 1 only if all inputs = 0.
- Q7: Complement of OR → NOR.
- Q8: XNOR = 1 when inputs are equal.
- Q9: OR can be built with 3 NANDs.
- Q10: XOR(1,0) = 1.
🎯 Motivation
Logic gates are the alphabet of digital electronics.
👉 Without them, microprocessors, memory, and controllers cannot be built.
👉 In ECET, 5–6 marks are directly asked from Boolean simplification and gate-level implementation.
👉 If you master this, digital design becomes very easy.
📲 CTA
👉 For more ECET 2026 Digital Electronics practice, join our free Telegram group for daily notes, quizzes & tips.
🔗 Join Here



