Concept Notes
1. Types of Number Systems
- Decimal (Base 10): Digits
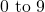. Example: 
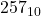. - Binary (Base 2): Digits
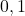. Example: 
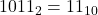. - Octal (Base 8): Digits
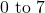. Example: 
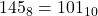. - Hexadecimal (Base 16): Digits
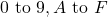. Example: 
.
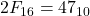2. Conversion Methods
a) Decimal → Any Base
Divide the number by base, collect remainders.
Example:
So,
.
b) Binary → Decimal
Multiply each bit by 
.
Example: 
c) Octal ↔ Binary
Each octal digit → 3 binary bits.
Example: 
.
d) Hexadecimal ↔ Binary
Each hex digit → 4 binary bits.
Example: 
.
3. Fractions Conversion
Decimal Fraction → Binary
Multiply fraction by 2, take integer part.
Example:
So
.
4. Complements
- 1’s complement: Replace 0 → 1, 1 → 0.
- 2’s complement: 1’s complement + 1.
- Used in binary subtraction.
⚙️ Important Formulas
Decimal to Binary:
Decimal to Octal:
Decimal to Hexadecimal:
Number of digits required in base r:
🔟 10 MCQs
Q1. 
= ? in decimal
a) 8
b) 9
c) 10
d) 11
Q2. 
= ? in binary
a) 
b) 
c) 
d) 
Q3. Which number system uses base 16?
a) Octal
b) Hexadecimal
c) Binary
d) Decimal
Q4. 
= ? in binary
a) 
b) 
c) 
d) 
Q5. 
= ? in decimal
a) 45
b) 46
c) 47
d) 48
Q6. 
= ? in octal
a) 45
b) 37
c) 25
d) 35
Q7. 1’s complement of 
is:
a) 
b) 
c) 
d) 
Q8. 2’s complement of 
is:
a) 
b) 
c) 
d) 
Q9. Number of digits required to represent 
in binary:
a) 7
b) 8
c) 9
d) 6
Q10. Decimal fraction 
= ? in binary
a) 
b) 
c) 
d) 
✅ Answer Key
| Q No | Answer |
|---|---|
| Q1 | c |
| Q2 | a |
| Q3 | b |
| Q4 | a |
| Q5 | c |
| Q6 | b |
| Q7 | a |
| Q8 | b |
| Q9 | b |
| Q10 | b |
🧠 Explanations
- Q1:
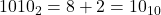. - Q2:
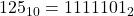. - Q3: Hexadecimal uses base 16.
- Q4:
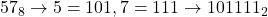. - Q5:
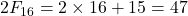. - Q6:
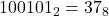. - Q7: 1’s complement = invert bits → .
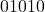- Q8: 2’s complement of
→ 0110+1 = 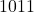. - Q9:
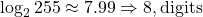. - Q10: From earlier example = .
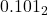🎯 Motivation
Number systems are the foundation of Digital Electronics.
- Every microprocessor/microcontroller uses binary, octal, and hex.
- In ECET, conversion & complements are repeated every year.
👉 Mastering them ensures free marks in the exam!
📲 CTA
👉 Practice daily ECET mock questions on our portal for Digital Electronics & get exam-ready.
🔗 Join Here
