In ECET 2026 Computer Science, Searching Algorithms are simple yet very scoring topics. Every year, 1–2 direct questions come from Linear Search and Binary Search. If you practice the logic and formulas properly, you can secure easy marks.
📘 Concept Notes
🔹 Linear Search
- Linear Search is the simplest searching technique.
- We compare the target element with each element in the list sequentially.
- Works on unsorted arrays.
- Time Complexity:
- Best Case =
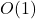 (if element found at first position)
(if element found at first position) - Worst Case =
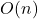 (if element is last or not found)
(if element is last or not found)
- Best Case =
- Algorithm Steps:
- Start from the first element.
- Compare it with the target element.
- If match found → return index.
- If end reached → element not found.
Example:
Array = [2, 5, 7, 9, 11], Target = 9
→ Compare one by one, found at index 3 (0-based indexing).
🔹 Binary Search
- Binary Search is faster but works only on sorted arrays.
- Process: Divide & Conquer.
- Compare target with middle element:
- If target = mid → found.
- If target < mid → search left half.
- If target > mid → search right half.
- Time Complexity:
- Best Case =
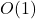
- Worst Case =
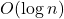
- Best Case =
- Algorithm Steps:
- Set low = 0, high = n-1.
- Repeat while low ≤ high:
- mid = (low + high)/2
- If arr[mid] == target → found.
- Else if arr[mid] > target → high = mid – 1.
- Else low = mid + 1.
Example:
Array = [2, 5, 7, 9, 11, 15, 20], Target = 15
- mid = 7 (arr[3] = 9), 15 > 9 → search right half
- New mid = arr[5] = 15 → Found at index 5.
⚙️ Formulas
- Linear Search Complexity:
![]()
Binary Search Complexity:
![]()
🔟 10 Most Expected MCQs – ECET 2026
Q1. Linear Search works on:
A) Sorted arrays only
B) Unsorted arrays only
C) Both sorted & unsorted arrays
D) None
Q2. Worst case time complexity of Linear Search is:
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Q3. Binary Search requires:
A) Random access
B) Sorted array
C) Sequential access
D) Unsorted array
Q4. Which is faster for large data?
A) Linear Search
B) Binary Search
C) Both same
D) None
Q5. Best case complexity of Binary Search:
A) ![]()
B) ![]()
C) ![]()
D) None
Q6. If array size is 1024, maximum comparisons in Binary Search = ?
A) 10
B) 11
C) 1024
D) 512
Q7. Which algorithm follows Divide & Conquer?
A) Linear Search
B) Binary Search
C) Both
D) None
Q8. Linear Search in best case requires:
A) 1 comparison
B) ![]() comparisons
comparisons
C) ![]() comparisons
comparisons
D) 2 comparisons
Q9. Binary Search is not suitable for:
A) Large sorted arrays
B) Linked lists
C) Random access memory
D) None
Q10. For array size n, Binary Search maximum comparisons = ?
A) ![]()
B) ![]()
C) ![]()
D) 1
✅ Answer Key (Table format – WordPress friendly)
| Q.No | Answer |
|---|---|
| Q1 | C |
| Q2 | B |
| Q3 | B |
| Q4 | B |
| Q5 | A |
| Q6 | B |
| Q7 | B |
| Q8 | A |
| Q9 | B |
| Q10 | A |
🧠 Explanations
- Q1 → C: Linear search checks one by one, so works on both sorted & unsorted arrays.
- Q2 → B: Worst case → all n elements checked.
- Q3 → B: Binary search requires array to be sorted.
- Q4 → B: Binary search is much faster than linear for large n.
- Q5 → A: If found at mid in first step → O(1).
- Q6 → B:
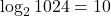 , so max = 11 comparisons.
, so max = 11 comparisons. - Q7 → B: Binary search uses divide & conquer.
- Q8 → A: Best case = first element match → only 1 comparison.
- Q9 → B: Binary search needs random access, linked list doesn’t support.
- Q10 → A: Max comparisons =
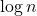 .
.
🎯 Why Practice Matters for ECET 2026
Linear and Binary Search are guaranteed topics in ECET exams.
- Questions are direct, mostly formula or logic-based.
- Helps build strong basics for advanced searching and sorting algorithms.
- Mastering these ensures at least 2–3 marks in Data Structures section.
📲 Join Our ECET Prep Community on Telegram
👉 For daily MCQs, solved examples, and video sessions: @LearnNewThingsHub