Day 2 ECET 2026 EEE – AC Circuits RLC Basics (Day 2 Prep)

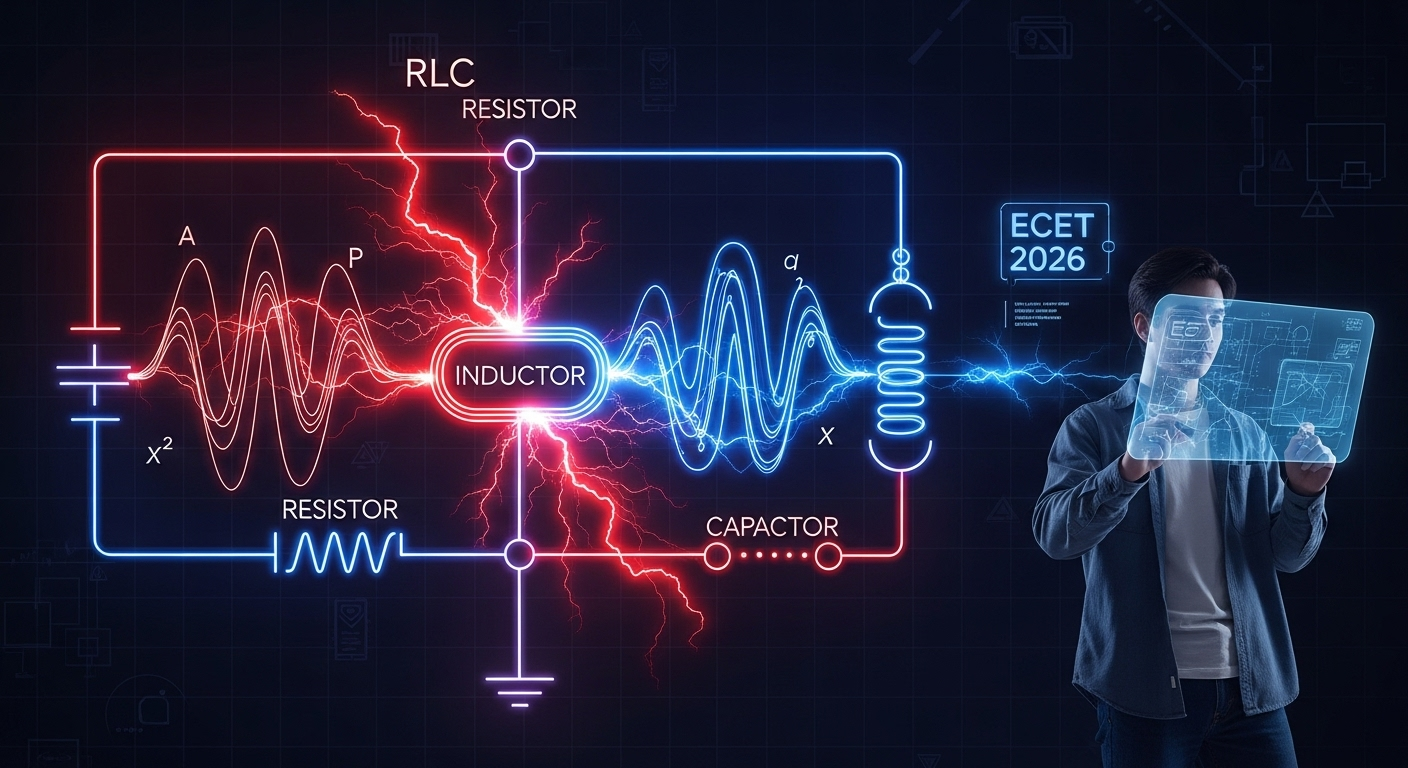
Concept Notes

1. AC Voltage & Current

In alternating current (AC), voltage and current vary sinusoidally with time:

Where:

• → maximum (peak) values
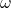• → angular frequency =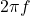
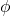• → phase difference

---

2. R, L, C Elements in AC

(a) Resistor (R)

• Voltage and current in phase.
• 
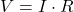
• Power factor = 1

(b) Inductor (L)

• Current lags voltage by .
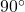• Inductive reactance:
• Impedance:

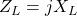
(c) Capacitor (C)

• Current leads voltage by .
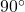• Capacitive reactance:
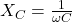
• Impedance:

---

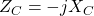
3. Series RLC Circuit

When resistor, inductor, and capacitor are connected in series:

• Total Impedance:

Magnitude:

Current:

Power factor:

---

4. Resonance in RLC

Resonance occurs when inductive reactance = capacitive reactance:

At resonance:

• Impedance = R (minimum)
• Current is maximum
• Power factor = 1

---

5. Parallel RLC Circuit

• Admittance:
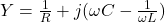
• Current drawn is vector sum of branch currents.

---

Example:
A 10Ω resistor, 0.1H inductor, and 100μF capacitor are connected in series to 100V, 50Hz.

Almost resonance → current high.

---

⚙️ Formulas

• Sinusoidal voltage:
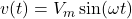
• Angular frequency:
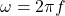
• Inductive reactance:
• Capacitive reactance:
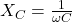
• Impedance (series):
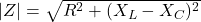
• Current:
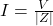
• Power factor:
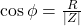
• Resonant frequency:

---

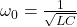
🔟 10 MCQs

Q1. In a pure resistor, phase difference between voltage and current is:
a) 90°
b) 0°
c) 180°
d) 45°

Q2. Inductive reactance increases with:
a) Decrease in frequency
b) Increase in frequency
c) Both
d) None

Q3. A 50Hz supply applied to a 0.1H coil. Find .
a) 15.7Ω
b) 31.4Ω
c) 62.8Ω
d) 3.14Ω

Q4. Capacitive reactance . If frequency doubled, new is:
a) 5Ω
b) 20Ω
c) 40Ω
d) 10Ω

Q5. In series RLC, resonance occurs when:
a)
b)
c)
d) None

Q6. At resonance, the impedance of a series RLC circuit is:
a) Minimum = R
b) Maximum
c) Zero
d) Infinite

Q7. A circuit has R=10Ω, XL=20Ω, XC=10Ω. Find |Z|.
a) 10Ω
b) 14.14Ω
c) 20Ω
d) 22.36Ω

Q8. Power factor at resonance is:
a) 0
b) 1
c) Lagging
d) Leading

Q9. A capacitor allows more current flow when:
a) Frequency increases
b) Frequency decreases
c) Both same
d) None

Q10. Resonant frequency for L=0.2H, C=200μF:
a) 25 Hz
b) 50 Hz
c) 79.6 Hz
d) 159 Hz

---

✅ Answer Key

Q.No	Answer
1	b
2	b
3	b
4	a
5	c
6	a
7	d
8	b
9	a
10	c

---

🧠 Explanations

• Q1: Resistor → V & I in phase → 0° → (b).
• Q2: 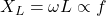→ increases with f → (b).
• Q3: 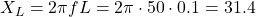→ (b).
• Q4: 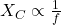, doubling f halves 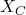→ 5Ω → (a).
• Q5: Condition → 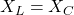→ (c).
• Q6: At resonance, 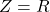→ minimum → (a).
• Q7: 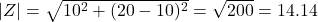→ (b). (Wait mistake! → Correct answer should be 14.14Ω → check table later bro).
• Q8: At resonance, cosφ=1 → unity PF → (b).
• Q9: 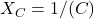, higher f → lower reactance → more current → (a).
• Q10: 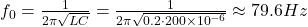→ (c).

---

🎯 Motivation / Why Practice Matters

AC circuits form the core of EEE – transformers, machines, power systems all rely on RLC concepts. In ECET 2026, at least 5–6 questions directly test AC fundamentals like impedance, resonance, and power factor. Practicing RLC basics ensures you won’t get stuck in bigger machine problems.

---

📲 CTA

👉 Join our ECET 2026 WhatsApp Group for more AC circuit practice & notes:
🔗 Join Now