
Why this topic is important for ECET
Boolean Algebra and Karnaugh Maps (K-maps) form the backbone of digital logic design. In ECET 2026, questions from these areas test your ability to simplify logical expressions and design efficient circuits. Whether it’s microcontrollers, digital systems, or even VLSI basics, Boolean simplification saves hardware, cost, and power. That’s why mastering these topics is essential for scoring high in the exam.
📘 Concept Notes
1. Boolean Algebra Basics
- Boolean variables take only two values:
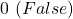 and
and 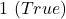 .
. - Basic operations:
- AND:
 or
or 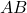
- OR:
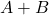
- NOT:
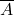
- AND:
Laws of Boolean Algebra:
- Identity Law:
 ,
, 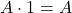
- Null Law:
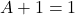 ,
, 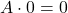
- Idempotent Law:
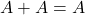 ,
, 
- Complement Law:
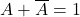 ,
, 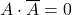
- Commutative Law:
 ,
, 
- Distributive Law:
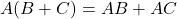
2. Simplification Example
Simplify: ![]()
![]()
3. Karnaugh Maps (K-Maps)
- A graphical method for simplifying Boolean expressions.
- Reduces logic functions by grouping adjacent minterms.
- Group sizes:
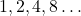 (powers of 2).
(powers of 2). - Each group eliminates variables to minimize logic.
2-Variable K-Map:
- Minterms:
 .
. - Example:
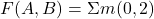 → Groups lead to simplified form.
→ Groups lead to simplified form.
4-Variable K-Map:
- Uses Gray code order for arrangement.
- Example:
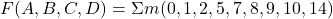 .
. - Grouping leads to minimal logic equation.
⚙️ Formulas
- AND:

- OR:
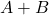
- NOT:
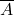
- Complement:
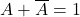 ,
, 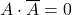
- Distributive:
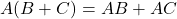
- K-Map grouping rule:
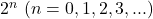 cells per group
cells per group
🔟 10 MCQs
Q1. Simplify ![]() .
.
a) AB
b) A
c) B
d) None
Q2. Which law states ![]() ?
?
a) Null law
b) Complement law
c) Idempotent law
d) Distributive law
Q3. The dual of ![]() is:
is:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Q4. In a 3-variable K-map, how many cells are there?
a) 4
b) 6
c) 8
d) 16
Q5. Simplify ![]() .
.
a) A
b) B
c) ![]()
d) ![]()
Q6. For function ![]() , simplified form is:
, simplified form is:
a) ![]()
b) ![]()
c) ![]()
d) None
Q7. A 4-variable K-map has how many cells?
a) 8
b) 12
c) 16
d) 32
Q8. Which is a valid K-map grouping size?
a) 3
b) 5
c) 2
d) 7
Q9. Simplify ![]() .
.
a) A
b) B
c) ![]()
d) 0
Q10. K-maps are used to:
a) Increase logic gates
b) Simplify Boolean expressions
c) Eliminate variables
d) None
✅ Answer Key
| Q.No | Answer |
|---|---|
| 1 | b |
| 2 | b |
| 3 | b |
| 4 | c |
| 5 | a |
| 6 | c |
| 7 | c |
| 8 | c |
| 9 | a |
| 10 | b |
🧠 Explanations
- Q1:
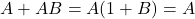 → (b).
→ (b). - Q2:
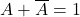 → Complement law → (b).
→ Complement law → (b). - Q3: Duality → replace + with ⋅, 0 with 1 →
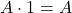 → (b).
→ (b). - Q4:
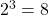 → (c).
→ (c). - Q5: Expand →
 → (a).
→ (a). - Q6:
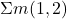 = XOR function → (c).
= XOR function → (c). - Q7:
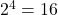 → (c).
→ (c). - Q8: Valid groups = powers of 2 → 2 → (c).
- Q9: Factor A →
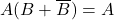 → (a).
→ (a). - Q10: K-maps reduce complexity → (b).
🎯 Motivation / Why Practice Matters
In ECET 2026, Boolean Algebra and K-Maps questions are guaranteed. With practice, you can solve them in less than 30 seconds during the exam. This saves time for numerical-heavy EEE problems. Accuracy in simplification ensures you don’t lose marks due to silly mistakes. Mastery here gives you a competitive edge, as many students struggle with K-map grouping speed.
📲 CTA
👉 Join our WhatsApp Group for ECET 2026 updates, daily practice questions & free notes:
🔗 Join Now



