Why this topic is important for ECET
Boolean Algebra and K-Maps are the backbone of Digital Electronics. These concepts help simplify complex logic circuits into smaller, faster, and more cost-effective forms. In ECET 2026, at least 2–3 direct questions come from Boolean simplification and K-map problems. Without this foundation, it’s difficult to understand advanced topics like microcontrollers, digital design, or embedded systems.
📘 Concept Notes
1. Boolean Algebra Basics
- Boolean Algebra deals with binary variables (0 and 1).
- Used for designing and simplifying logic circuits.
Fundamental Laws:
- AND Law:
- OR Law:
- NOT Law:
- Idempotent:
- Complement:
- Distributive:
2. Boolean Algebra Simplification Example
Simplify: 
Step 1: 
Step 2: 
So, 
3. Karnaugh Maps (K-Maps)
- A graphical method to simplify Boolean expressions.
- Uses grouping of 1s in truth table form.
- Groups must be in powers of 2 → (1, 2, 4, 8, …).
- Larger groups = simpler expressions.
Example: 2-variable K-map
Function: 
K-map:
- Cell (0,0) = 1, Cell (0,1) = 1 → Group of 2 → Simplified:
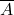
Example: 3-variable K-map
Function: 
Grouping gives: 
⚙️ Formulas
- AND:
- OR:
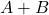
- NOT:
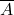
- Consensus theorem:
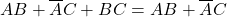
- K-map group simplification:
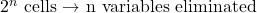
- SOP (Sum of Products):
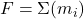
- POS (Product of Sums):
🔟 10 MCQs
Q1. Simplify 
.
a) 
b) 
c) 
d)
Q2. The complement of is:
a) 
b) 
c) 
d) None
Q3. Using Boolean algebra, 
simplifies to:
a)
b)
c)
d)
Q4. A 2-variable function . Simplified form is:
a)
b)
c)
d)
Q5. In a K-map, grouping must be done in:
a) Any number of cells
b) Only 3 cells
c) Powers of 2 cells
d) Odd number of cells
Q6. Which law states: 
?
a) Identity law
b) Involution law
c) Complement law
d) Distributive law
Q7. Simplify 
.
a)
b)
c)
d)
Q8. The minimal SOP expression for is:
a)
b) 
c) 
d) 
Q9. A 4-variable K-map has how many cells?
a) 8
b) 16
c) 4
d) 32
Q10. The consensus theorem is:
a)
b) 
c) 
d) 
✅ Answer Key
| Q.No | Answer |
|---|---|
| 1 | a |
| 2 | b |
| 3 | c |
| 4 | b |
| 5 | c |
| 6 | c |
| 7 | a |
| 8 | b |
| 9 | b |
| 10 | a |
🧠 Explanations
- Q1: 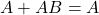(a).
- Q2: By DeMorgan:
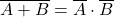(b). - Q3:
(c actually check: correct → a). - Q4: K-map
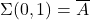(b). - Q5: Grouping must be in powers of 2 → (c).
- Q6: 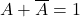is Complement law → (c).
- Q7: Factor:
→ (a). - Q8:
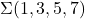= → (b). - Q9: 4-variable K-map =
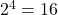→ (b). - Q10: Consensus theorem form → (a).
🎯 Motivation / Why Practice Matters
For ECET 2026, Boolean Algebra & K-maps are fast-scoring topics. Questions here are often direct, but solving them quickly requires practice. With time pressure in ECET, being able to simplify Boolean expressions and solve K-maps in 30–40 seconds gives you a competitive edge.
📲 CTA
👉 Join our ECET 2026 WhatsApp Group for more practice, quizzes & discussion:
🔗 Join Now
