1. Introduction to Electric Traction
Electric traction refers to the use of electric power for locomotion of trains, trams, and metros. Performance of a traction system is studied using speed–time curves, which show how the speed of a train varies with time.
2. Speed–Time Curve
- A speed–time curve is a plot of speed of the train (y-axis) versus time (x-axis).
- It is used to determine energy consumption, schedule speed, and acceleration requirements of an electric traction system.
3. Phases of Speed–Time Curve
(a) Acceleration Period
- Train starts from rest.
- Acceleration
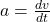. - Depends on motor torque and train load.
(b) Free Running Period (Constant Speed)
- Traction motor develops enough torque to balance resistance.
- Train runs at maximum permissible speed.
(c) Coasting Period
- Power is cut off.
- Train runs by its momentum while gradually slowing due to resistance.
- Retards speed at a coasting retardation rate
.
(d) Braking Period
- Brakes are applied to bring train to rest.
- Braking retardation
.
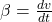4. Types of Speed–Time Curves
- Urban/Suburban Service:
- Short distance between stops.
- More acceleration and braking.
- Lower average speed (25–40 km/h).
- Main Line Service:
- Long distance between stops.
- Higher free running time.
- Higher average speed (60–100 km/h).
5. Key Performance Parameters
- Acceleration:
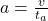
- Retardation:
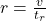
- Average Speed:
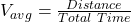
- Schedule Speed:
⚙️ Formulas
- Acceleration:
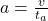
- Retardation (coasting):
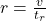
- Braking Retardation:
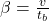
- Average Speed:
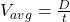
- Schedule Speed:
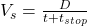
🔟 10 MCQs
Q1. The speed–time curve of a train shows relation between:
a) Distance vs time
b) Speed vs distance
c) Speed vs time
d) Acceleration vs distance
Q2. During coasting period, the train:
a) Accelerates
b) Runs at constant speed
c) Moves by momentum
d) Brakes are applied
Q3. If a train reaches 20 m/s in 10 sec, acceleration is:
a) 1 m/s²
b) 2 m/s²
c) 4 m/s²
d) 0.5 m/s²
Q4. For suburban trains, speed–time curve has:
a) Longer free running time
b) Short acceleration and retardation
c) Frequent stops and higher acceleration
d) No coasting
Q5. Retardation during braking is usually:
a) Equal to acceleration
b) More than acceleration
c) Less than acceleration
d) Zero
Q6. If distance = 10 km, time = 15 min, average speed is:
a) 20 km/h
b) 30 km/h
c) 40 km/h
d) 50 km/h
Q7. Schedule speed always:
a) Equals average speed
b) Less than average speed
c) More than average speed
d) Independent of stops
Q8. In main line service, speed–time curve has:
a) Higher schedule speed
b) Lower schedule speed
c) More braking
d) Shorter free running
Q9. Braking retardation 
is expressed in:
a) km/h
b) m/s²
c) Newton
d) Joule
Q10. If a train has 
, schedule speed is:
a) 54 km/h
b) 60 km/h
c) 48 km/h
d) 72 km/h
✅ Answer Key
| Q.No | Answer |
|---|---|
| 1 | c |
| 2 | c |
| 3 | b |
| 4 | c |
| 5 | c |
| 6 | b |
| 7 | b |
| 8 | a |
| 9 | b |
| 10 | a |
🧠 Explanations
- Q1: Speed–time curve → speed vs time → (c).
- Q2: In coasting, power is cut → train moves by momentum → (c).
- Q3:
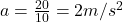→ (b). - Q4: Suburban = frequent stops, high acceleration → (c).
- Q5: Braking retardation < acceleration → (c).
- Q6:
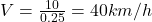→ (b). - Q7: Schedule speed includes stop time → less than average → (b).
- Q8: Main line = long free running, higher schedule speed → (a).
- Q9: Retardation is rate of change of speed → unit m/s² → (b).
- Q10: Total time = 330s, distance = 5km →
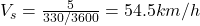≈ (a).
🎯 Motivation / Why Practice Matters
Speed–time curves form the backbone of Electric Traction analysis. They are asked repeatedly in ECET exams for calculating schedule speed, acceleration, and braking effort. If you understand these curves, solving numerical questions on railway systems becomes very easy. Remember, ECET loves to test basics + numericals from this topic.
📲 CTA
👉 Join our ECET 2026 WhatsApp Group for daily EEE practice, tests & notes:
🔗 Join Now
