Concept Notes
1. Introduction to Logic Gates
Digital systems work on binary signals (0 and 1). Logic gates are the basic building blocks of digital circuits.
- Input: Binary (0 or 1)
- Output: Binary (0 or 1)
- Implemented using electronic switches (transistors, diodes, MOSFETs).
The three basic gates are: AND, OR, NOT. All other complex gates (NAND, NOR, XOR, XNOR) are derived from these.
2. AND Gate
- Symbol:
D-shapedwith multiple inputs. - Operation: Output is 1 only if all inputs are 1.
Boolean Expression:
Truth Table:
| A | B | Y = A·B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Example:
If two switches are in series, both must be ON (1) for the lamp to glow → AND operation.
3. OR Gate
- Symbol: Curved shape with multiple inputs.
- Operation: Output is 1 if any one input is 1.
Boolean Expression:
Truth Table:
| A | B | Y = A + B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Example:
If two switches are in parallel, closing any switch (1) makes the lamp glow → OR operation.
4. NOT Gate
- Symbol: Triangle with a bubble at output.
- Operation: Produces the complement of input.
Boolean Expression:
Truth Table:
| A | Y = NOT A |
|---|---|
| 0 | 1 |
| 1 | 0 |
Example:
A switch connected with inverter circuit → If switch is ON (1), output is OFF (0).
5. Importance for ECET
- Logic gates are the foundation for digital circuits, microcontrollers, PLCs, and processors.
- Complex problems in ECET like simplification, Boolean algebra, K-map minimization are based on these basics.
⚙️ Formulas
- AND Gate:
- OR Gate:
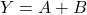
- NOT Gate:
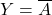
🔟 10 MCQs
Q1. Output of AND gate is 1 when:
a) Any input is 1
b) All inputs are 1
c) All inputs are 0
d) None
Q2. Output of OR gate is 0 when:
a) All inputs are 0
b) Any input is 1
c) All inputs are 1
d) Any input is 0
Q3. NOT gate is also called:
a) Buffer
b) Inverter
c) Comparator
d) Multivibrator
Q4. Boolean expression of OR gate is:
a) 
b) 
c) 
d) None
Q5. Truth table of AND gate has how many input combinations (for 2 inputs)?
a) 2
b) 3
c) 4
d) 8
Q6. If 
, output of is:
a) 0
b) 1
c) Undefined
d) None
Q7. Which gate is used to perform multiplication in Boolean algebra?
a) OR
b) AND
c) NOT
d) XOR
Q8. Which gate gives the complement of the input?
a) AND
b) OR
c) NOT
d) NAND
Q9. Simplify: 
a) 1
b) 0
c) A
d) None
Q10. In a microcontroller, basic logic decisions are made using:
a) Counters
b) Flip-flops
c) Logic gates
d) Registers
✅ Answer Key
| Q.No | Answer |
|---|---|
| 1 | b |
| 2 | a |
| 3 | b |
| 4 | b |
| 5 | c |
| 6 | b |
| 7 | b |
| 8 | c |
| 9 | c |
| 10 | c |
🧠 Explanations
- Q1: AND → output 1 only if all inputs 1 → (b).
- Q2: OR → output 0 only if all inputs 0 → (a).
- Q3: NOT = Inverter → (b).
- Q4: OR = 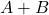→ (b).
- Q5: For 2 inputs →
combinations → (c). - Q6:
→ (b). - Q7: Boolean multiplication = AND → (b).
- Q8: Complement of input → NOT gate → (c).
- Q9: Double negation →
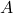→ (c). - Q10: Logic decisions → Logic gates → (c).
🎯 Motivation / Why Practice Matters
Logic gates may look simple, but every digital device (from calculators to microcontrollers and PLCs) is built using them. In ECET 2026, digital questions always start with basic gate problems. If you’re strong here, K-map, minimization, flip-flops, counters, and microcontroller logic become super easy.
📲 CTA
👉 Join our dedicated ECET 2026 WhatsApp Group for daily practice, notes & quizzes:
🔗 Join Now
