Day 51 – Morning Session: Graph Theory – Types of Graphs & Basics – ECET 2026

Graph Theory is one of the most important topics in Discrete Mathematics. In ECET 2026, you can expect 1–2 direct questions on graphs, degree formulas, and basic graph properties.

---

📘 Concept Notes – Basics of Graphs

🔹 Definition of Graph

A graph G is defined as:

Where:

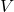• = set of vertices (or nodes)
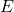• = set of edges (connections between vertices)

---

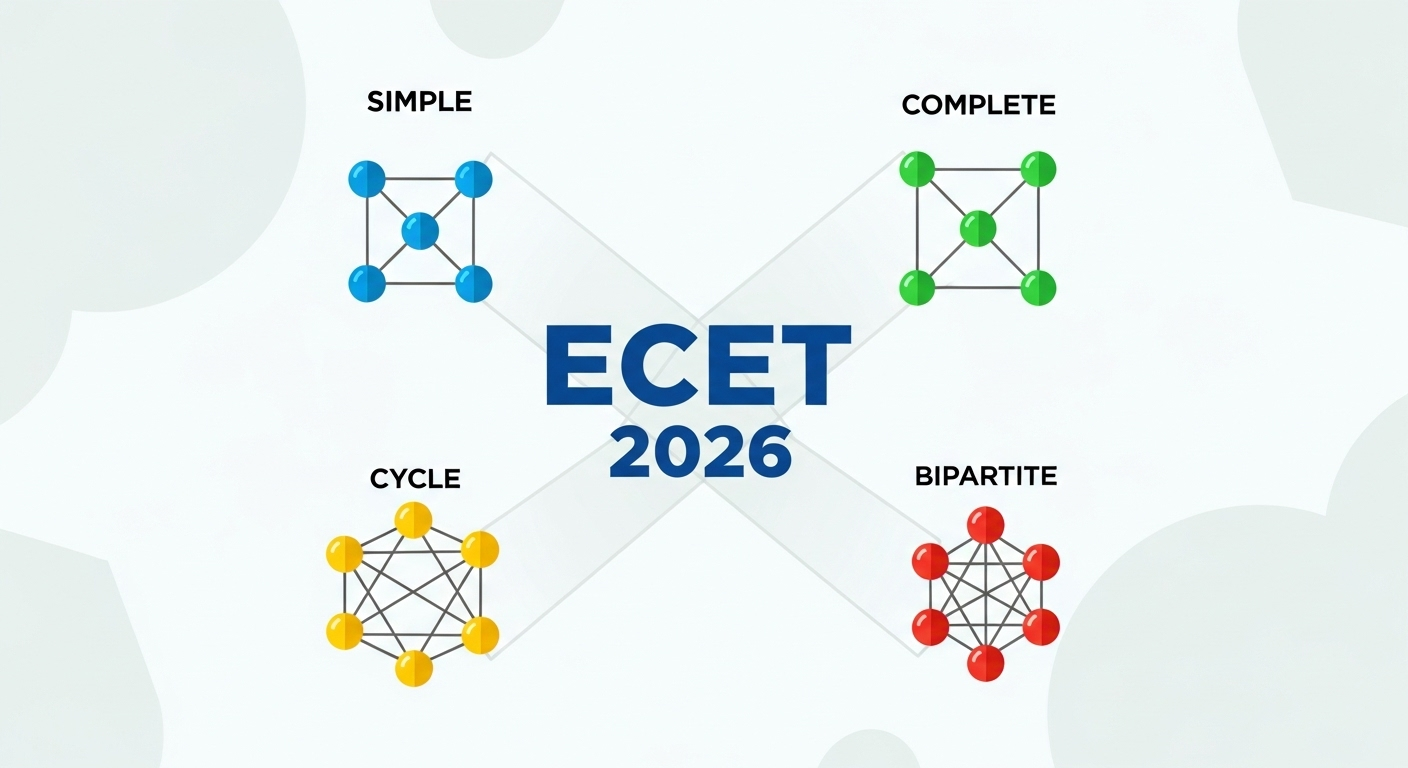
🔹 Types of Graphs

1. Simple Graph – No self-loops, no parallel edges.
2. Multi Graph – Multiple edges between the same pair of vertices.
3. Null Graph – Graph with only vertices, no edges.
4. Complete Graph (Kn) – Every pair of vertices is connected.
   • Number of edges:

Regular Graph – All vertices have the same degree.

Bipartite Graph – Vertices divided into 2 disjoint sets, edges only between sets.

Cycle Graph (Cn) – Graph forming a cycle with n vertices.

Path Graph (Pn) – Graph forming a simple path.

Weighted Graph – Edges carry weights (cost, distance, etc.).

Directed Graph (Digraph) – Edges have direction.

Undirected Graph – Edges have no direction.

---

⚙️ Important Formulas

1. Handshaking Lemma (Sum of Degrees):

Edges in Complete Graph:

Edges in Complete Bipartite Graph:
If partitions have and vertices:

---

📐 Example

• Consider a graph with 4 vertices forming a complete graph .
• Number of edges = .
• Degree of each vertex = .
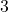• Sum of degrees = 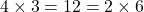✔️ (Handshaking Lemma holds).

---

🔟 10 Expected MCQs – ECET 2026

Q1. A graph with only vertices and no edges is called:
A) Simple Graph
B) Null Graph
C) Complete Graph
D) Multi Graph

Q2. Number of edges in a complete graph is:
A)
B)
C)
D)

Q3. A graph where every vertex has equal degree is:
A) Null Graph
B) Regular Graph
C) Complete Graph
D) Bipartite Graph

Q4. Which graph is used to represent two disjoint sets?
A) Cycle Graph
B) Bipartite Graph
C) Path Graph
D) Multi Graph

Q5. In , the number of edges is:
A) 5
B) 8
C) 10
D) 12

Q6. The sum of degrees of all vertices in a graph is always:
A) Equal to number of edges
B) Twice the number of edges
C) Half the number of edges
D) Depends on graph type

Q7. Which graph has exactly edges?
A) Null Graph
B) Tree
C) Complete Graph
D) Path Graph

Q8. A graph with edges having weights is called:
A) Simple Graph
B) Multi Graph
C) Weighted Graph
D) Directed Graph

Q9. A cycle with 4 vertices is denoted as:
A)
B)
C)
D)

Q10. If a bipartite graph has partitions with 3 and 4 vertices, number of edges is:
A) 7
B) 10
C) 12
D) 14

---

✅ Answer Key

Q.No	Answer
Q1	B
Q2	B
Q3	B
Q4	B
Q5	C
Q6	B
Q7	B
Q8	C
Q9	A
Q10	C

---

🧠 Explanations

• Q1 → B: Graph with no edges = Null Graph.
• Q2 → B: Complete graph edges = .
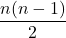• Q3 → B: Regular graph = equal degree vertices.
• Q4 → B: Bipartite = 2 disjoint sets.
• Q5 → C: 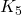edges = .
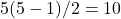• Q6 → B: Handshaking lemma → sum of degrees = 2 × edges.
• Q7 → B: Trees have edges.
• Q8 → C: Weighted graph → edges with weights.
• Q9 → A: Cycle graph with 4 vertices = .
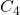• Q10 → C: Complete bipartite edges = .

---

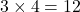🎯 Why Practice Matters

• Graph theory is highly scoring in ECET.
• Formulas like handshaking lemma and complete graph edges are direct MCQs.
• Visualizing examples (K4, Cn, Pn) helps solve problems quickly.

---

📲 Join Our ECET Prep Community on WhatsApp

👉 Join WhatsApp Group – Click Here