In ECET 2026 Mathematics, Applications of Integrals is one of the most important calculus topics. It mainly deals with finding areas under curves and areas between two curves. These questions appear frequently and are easy-scoring if you understand the geometry and integration concepts.
📘 Concept Notes – Applications of Integrals
🔹 What Are Applications of Integrals?
Integrals are used to calculate:
- Area under a curve
- Area between two curves
- Area bounded by curves and coordinate axes
The area is always considered positive, and integration helps to sum infinitely small strips to get total area.
⚙️ Formulas (in QuickLaTeX format)
1️⃣ Area under a curve (y = f(x)) between x = a and x = b:
2️⃣ Area between two curves (y = f(x) and y = g(x)):
![A = \int_{a}^{b} [f(x) - g(x)] , dx](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-84bc9625bac7f6c8d1c88631253109be_l3.png "Rendered by QuickLaTeX.com")
Here, 
in [a, b].
3️⃣ Area between a curve and x-axis (if curve lies below x-axis):
4️⃣ Area between two curves given as x = f(y) and x = g(y):
![A = \int_{y_1}^{y_2} [f(y) - g(y)] , dy](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-349e0a915051982c95b01969d4b1fedf_l3.png "Rendered by QuickLaTeX.com")
📐 Examples
Example 1:
Find the area bounded by the curve 
and the line 
.
Solution:
For intersection points:
Area =
= ![\left[ 4x - \frac{x^3}{3} \right]_{-2}^{2}](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-3d007a0350b6904ea915a374125e0c44_l3.png "Rendered by QuickLaTeX.com")
= 
= 
✅ Answer: 
Example 2:
Find the area between curves 
and .
Solution:
Points of intersection: 
and 
Area =
= ![\left[ \frac{x^2}{2} - \frac{x^3}{3} \right]_{0}^{1}](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-f0481f54cfe0b3ff4e1ee901d5b3f993_l3.png "Rendered by QuickLaTeX.com")
= 
✅ Answer: 
Example 3:
Find the area enclosed by 
and 
.
Solution:
Convert limits: 
to
Area =
= ![\left[ 4y - \frac{y^3}{12} \right]_{-4}^{4}](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-14a0fd4dbc3a154c46b663d6b36f6969_l3.png "Rendered by QuickLaTeX.com")
= 
= 
✅ Answer: 
🔟 10 Most Expected MCQs – ECET 2026 (Applications of Integrals)
Q1. The area under y = f(x) from x = a to x = b is given by:
A) 
B) 
C) 
D) None
Q2. If the curve lies below the x-axis, the area is found using:
A)
B) 
C) 
D) 
Q3. The area between y = x and y = x² from x = 0 to x = 1 is:
A) 
B) 
C) 
D) 
Q4. The intersection points of y = x² and y = 4 are:
A) -2, 2
B) -1, 1
C) 0, 2
D) 1, 4
Q5. The area under y = x³ between x = 0 and x = 2 is:
A) 
B) 
C) 
D)
Q6. The area bounded by y = x² and y = 0 from x = 0 to x = 1 is:
A)
B)
C) 
D) 
Q7. The formula for area between curves x = f(y) and x = g(y) is:
A) ![\int_{x_1}^{x_2} [f(y) - g(y)] , dx](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-b289efb16e37e7c208ab0e412255794a_l3.png "Rendered by QuickLaTeX.com")
B) ![\int_{y_1}^{y_2} [f(y) - g(y)] , dy](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-0998c11c070489511ebdc49bfa433882_l3.png "Rendered by QuickLaTeX.com")
C) ![\int [f(x) + g(x)]](https://learnnewthings.fun/wp-content/ql-cache/quicklatex.com-4f769dfb0e52685f1d331288ef9b882c_l3.png "Rendered by QuickLaTeX.com")
D) None
Q8. The area under y = sin(x) from 0 to π is:
A) 
B)
C)
D) 
Q9. The integral 
represents:
A) Area under y = x²
B) Volume under y = x²
C) Slope of curve
D) None
Q10. If area between two curves is negative, actual area is:
A) Negative
B) Positive
C) Zero
D) Imaginary
✅ Answer Key
| Q.No | Answer |
|---|---|
| Q1 | B |
| Q2 | B |
| Q3 | B |
| Q4 | A |
| Q5 | C |
| Q6 | A |
| Q7 | B |
| Q8 | C |
| Q9 | A |
| Q10 | B |
🧠 Explanations
- Q1 → B: The correct direction for integration is from a → b.
- Q2 → B: Area is always positive, hence |f(x)|.
- Q3 → B: Area = .
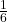- Q4 → A: From y = 4 ⇒ x² = 4 ⇒ x = ±2.
- Q5 → C:
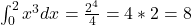. - Q6 → A:
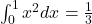. - Q7 → B: Integration with respect to y.
- Q8 → C:
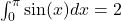. - Q9 → A: Area under y = x².
- Q10 → B: Area is taken as positive.
🎯 Why Practice Matters
- Applications of Integrals problems test both concept and calculation.
- Mastering formulas and graph visualization ensures full marks in this section.
- Area problems are among the most repeated ECET questions.
