Day 36 – Morning Session: Maths – Maxima & Minima Word Problems – ECET 2026

In ECET exams, questions on Maxima & Minima are commonly asked from Applied Calculus. They are mostly in the form of word problems where you need to optimize (maximize or minimize) a given quantity such as area, volume, cost, or profit.

---

📘 Concept Notes

🔹 Step-by-Step Method to Solve Maxima/Minima Word Problems

1. Define the variables from the problem.
2. Form an equation for the quantity to be optimized (objective function).
3. If constraints are given, eliminate extra variables using them.
4. Differentiate the objective function:

Solve to get critical points.

Use second derivative test:

• If → Minimum
• If 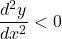→ Maximum

---

⚙️ Important Formulas

• First Derivative Condition:

Second Derivative Test:

For word problems:

---

📐 Examples

Example 1: Rectangle with maximum area
A rectangle is inscribed under a parabola on the x-axis. Find the maximum area.

• Let rectangle extend from 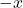to .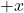
• Width = 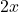, Height = .
• Area = .
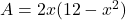• Differentiate: .
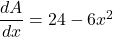• Set .
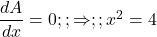• At 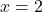, maximum area = .

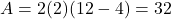Example 2: Box with minimum surface area
Find the dimensions of a cube of volume with minimum surface area.

• Let side = .
• Volume: .
• Surface area = .
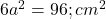• A cube gives minimum surface area for a given volume.

---

🔟 10 Expected MCQs – ECET 2026

Q1. Maxima and Minima problems are solved using:
A) Differentiation
B) Integration
C) Probability
D) Matrices

Q2. If and , the function has:
A) Minimum
B) Maximum
C) Saddle point
D) None

Q3. For maximum area, a rectangle under has width:
A) 2
B) 4
C) 8
D) 16

Q4. In optimization, the point where slope = 0 is called:
A) Inflection point
B) Critical point
C) Stationary point
D) Both B & C

Q5. A cube has minimum surface area among solids for:
A) Given perimeter
B) Given diagonal
C) Given volume
D) Given base

Q6. If , maximum area occurs at:
A)
B)
C)
D)

Q7. For , the maximum value is at:
A)
B)
C)
D) None

Q8. Second derivative test is used for:
A) Identifying critical points
B) Classifying maxima/minima
C) Finding slope
D) Integration

Q9. A rectangle of maximum area for given perimeter is:
A) Square
B) Circle
C) Rhombus
D) Triangle

Q10. If , local maxima is at:
A)
B)
C)
D)

---

✅ Answer Key

Q.No	Answer
Q1	A
Q2	B
Q3	B
Q4	D
Q5	C
Q6	B
Q7	A
Q8	B
Q9	A
Q10	C

---

🧠 Explanations

• Q1 → A: Optimization is solved using differentiation.
• Q2 → B: If second derivative < 0 → Maximum.
• Q3 → B: Width = 2x, max at .
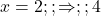• Q4 → D: Both stationary and critical point.
• Q5 → C: Cube gives min surface area for given volume.
• Q6 → B: At 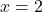, area maximum.
• Q7 → A: At 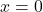, maximum.
• Q8 → B: Second derivative test classifies maxima/minima.
• Q9 → A: Square gives max area for fixed perimeter.
• Q10 → C: 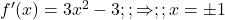. At 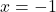, maxima.

---

🎯 Why Practice Matters

• Word problems on Maxima & Minima are scoring because they directly test calculus application.
• By practicing step-by-step, you can secure easy marks in ECET.

---

📲 Join Our ECET Prep Community on WhatsApp

👉 Join WhatsApp Group – Click Here