Day 48 – Morning Session: Mathematics – Mean Value Theorem (MVT) – ECET 2026

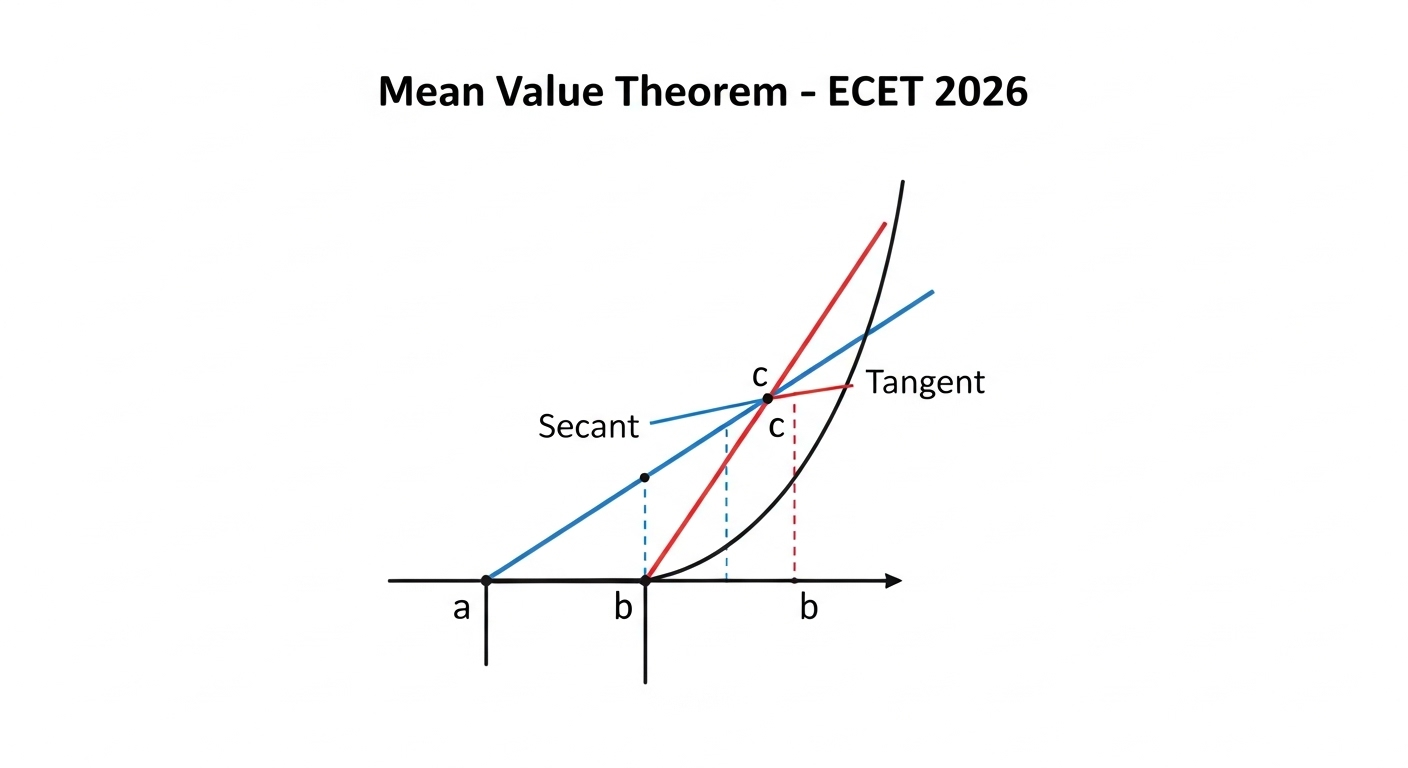
In ECET 2026 Mathematics, Calculus theorems like Rolle’s Theorem and Mean Value Theorem (MVT) are frequently tested. The Mean Value Theorem is one of the most fundamental results in differential calculus, often used in proofs and problem solving.

---

📘 Concept Notes – Mean Value Theorem

🔹 Statement of MVT

If:

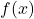1. is continuous on
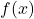2. is differentiable on

Then ∃ at least one point such that:

---

🔹 Geometric Meaning

• The theorem says: At some point, the tangent to the curve is parallel to the secant line joining 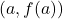and .

---

🔹 Relation with Rolle’s Theorem

• Rolle’s Theorem is a special case of MVT when .
• Then, 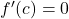for some .

---

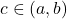⚙️ Key Formula

• General MVT condition:

• Slope of secant line:

• At some , slope of tangent:

---

📐 Example

Example 1:
Verify Mean Value Theorem for in .

1. Check conditions:
   • Continuous and differentiable (yes).
2. Compute slope of secant:

Differentiate:

Solve:

✅ Hence, MVT is satisfied at .

---

🔟 10 Expected MCQs – ECET 2026

Q1. The Mean Value Theorem requires function to be:
A) Continuous in [a, b]
B) Differentiable in (a, b)
C) Both A & B
D) None

Q2. If , MVT reduces to:
A) Rolle’s Theorem
B) Lagrange’s Theorem
C) Taylor’s Theorem
D) Cauchy’s Theorem

Q3. For on [1, 3], value of c that satisfies MVT is:
A) 1
B) 2
C) 3
D) None

Q4. If on [0, π], then slope of secant line is:
A) 0
B) 1
C) -1
D) None

Q5. Condition NOT required for MVT:
A) Continuity on [a, b]
B) Differentiability on (a, b)
C) f(a) = f(b)
D) None

Q6. For on [1, 2], slope of secant line is:
A) 5
B) 7
C) 9
D) 3

Q7. In MVT, the slope of tangent at c is:
A) Equal to slope of secant
B) Less than slope of secant
C) Greater than slope of secant
D) Independent

Q8. Rolle’s Theorem guarantees existence of:
A) f’(c) = slope of secant
B) f’(c) = 0
C) f(c) = 0
D) None

Q9. For on [1, e], slope of secant line is:
A) 0
B) 1
C) e
D) None

Q10. In MVT, the number of possible c values:
A) Always unique
B) At least one
C) Infinite
D) Zero

---

✅ Answer Key

Q.No	Answer
Q1	C
Q2	A
Q3	B
Q4	A
Q5	C
Q6	B
Q7	A
Q8	B
Q9	B
Q10	B

---

🧠 Explanations

• Q1 → C: Both conditions required.
• Q2 → A: Special case → Rolle’s Theorem.
• Q3 → B: c = 2 satisfies MVT.
• Q4 → A: .
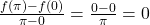• Q5 → C: f(a) = f(b) is for Rolle’s Theorem, not MVT.
• Q6 → B: .
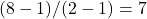• Q7 → A: By definition.
• Q8 → B: Rolle’s Theorem ensures f’(c) = 0.
• Q9 → B: .
• Q10 → B: At least one c exists.

---

🎯 Why Practice Matters

• MVT and Rolle’s Theorem are repeated exam topics.
• Questions are straightforward: slope, derivative, and verification.
• Practicing ensures quick marks in calculus section.

---

📲 Join Our ECET Prep Community on WhatsApp

👉 Join WhatsApp Group – Click Here