Mathematics lo Partial Fractions topic chala important for ECET exams. Polynomial fractions ni simpler fractions ga break cheyadam valla solving easy avutundi. Almost every year questions repeat avutayi, so ee concept ni master chesthe scoring easy.
📘 Concept Notes – Partial Fractions
Partial Fractions ante:
Oka rational function ni (numerator, denominator polynomial unna fraction) simpler fractions sum ga express cheyadam.
Types of Partial Fractions
1️⃣ Proper Fraction: Degree of numerator < Degree of denominator.
- Example:
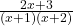
2️⃣ Improper Fraction: Degree of numerator ≥ Degree of denominator.
- First long division cheyyali, taruvata partial fractions apply cheyyali.
Standard Forms
- If denominator has distinct linear factors:
If denominator has repeated linear factors:
If denominator has quadratic factors:
⚙️ Key Formulas
🔟 10 Most Expected MCQs – ECET 2026 Maths
Q1. 
ni partial fractions form lo rayandi.
A) 
B) 
C) 
D) None
Q2. Denominator lo repeated root unte 
ni express chesthe?
A) 
B) 
C) 
D) None
Q3. 
A) 
B) 
C) 
D) None
Q4. 
can be written as?
A) 
B) 
C) 
D) None
Q5. Which of the following is a correct form of partial fraction expansion of 
?
A) 
B) 
C) 
D) None
Q6. In 
, the values of A and B are obtained by:
A) Substitution method
B) Comparing coefficients
C) Both A & B
D) None
Q7. Degree condition for applying partial fractions:
A) 
B) 
C) Always possible
D) None
Q8. 
expansion form is:
A) 
B) 
C) 
D) None
Q9. Improper fractions ni first step lo ela treat chestaru?
A) Direct ga expand cheyyali
B) First Long Division chesi, remainder ni expand cheyyali
C) Ignore denominator
D) None
Q10. 
can be expressed as:
A) 
B) 
C) 
D) None
Answer Key
| Q.No | Answer |
|---|---|
| Q1 | B |
| Q2 | C |
| Q3 | A |
| Q4 | D |
| Q5 | C |
| Q6 | B |
| Q7 | A |
| Q8 | D |
| Q9 | C |
| Q10 | B |
Explanations of Answers
- Q1: Using standard form,
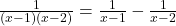. - Q2: For repeated root, always include .
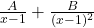- Q3: Cross-multiplication method →
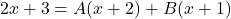→ A=2, B=1. - Q4:
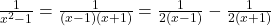. - Q5: Quadratic factor case → .
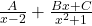- Q6: Either substitution (x=1,2) or comparing coefficients.
- Q7: Degree of numerator must be less.
- Q8: For repeated + distinct factors → .
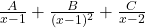- Q9: Improper fraction → do polynomial division first.
- Q10: Quadratic factor → .
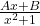🎯 Why This Practice Matters
Partial Fractions topic lo ECET lo direct ga 2–3 questions vastee chance ekkuva.
Practicing expansion techniques → fast solving + accuracy in exams.
Alage engineering lo Laplace transforms, integration lo kuda chala use untundi.
📲 Join Our ECET Prep Community
👉 For daily practice questions, solved problems & video sessions:
Telegram: @LearnNewThingsHub
