Day 71 Morning – Probability – Permutations & Combinations

Concept Notes (Deep Explanation + Examples)

🔹 Introduction

Probability, Permutations, and Combinations form the core of ECET Mathematics. Every year, 3–4 direct questions appear from these topics. Understanding these three concepts together helps in solving complex problems on probability and counting efficiently.

---

🔹 1. Basic Idea of Counting

Before learning probability, we must know how to count possible outcomes.

If one event can happen in m ways and another in n ways,
then both can happen in ways.
👉 This is called the Fundamental Principle of Counting (FPC).

Example:
A student can choose 3 shirts and 2 pants.
Total combinations = possible outfits.

---

🔹 2. Permutations

A permutation is an arrangement of objects in a specific order.

If n objects are taken r at a time,
number of permutations =

Example:
Number of ways to arrange 3 letters from A, B, C, D = .

🔸 Real-life Example (Coding):
Arranging passwords of 4 characters from A-Z → possible unique passwords.

---

🔹 3. Combinations

A combination is a selection of objects without considering order.

If n objects are taken r at a time,
number of combinations =

Example:
Selecting 3 members from 5 students = .

🔸 Real-life Example (Database / SQL):
Choosing 3 attributes out of 10 for a SELECT query = combinations problem.

---

🔹 4. Relationship Between Permutation and Combination

It means every combination can be arranged in r! different ways.

---

🔹 5. Probability

Probability = (Favourable Outcomes) / (Total Outcomes)

If an event E can happen in m ways and total outcomes are n,
then

---

🔹 6. Connecting Probability with Combinations

When the order doesn’t matter, use combinations for counting favorable cases.

Example:
Find the probability of drawing 2 hearts from a deck of 52 cards.

Favorable outcomes =
Total outcomes =
So,

---

🔹 7. Special Cases and Tricks

1. 
2. 
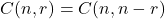
3. Total subsets of a set with n elements =
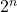
4. Probability of impossible event = 0
5. Probability of certain event = 1

---

🧮 Visual Diagram (explained in words)

Imagine a tree diagram:
Each branch splits for each possible choice (shirt → pant → shoe).
Counting all paths gives total outcomes.
In probability, we divide favorable paths by total paths.

---

3️⃣ ⚙️ Formulas (Plain LaTeX, No Boxes)

---

4️⃣ 🔟 10 MCQs (ECET + GATE Hybrid)

1. The number of permutations of the word “ECET” is:
   A) 12 B) 24 C) 8 D) 16
2. The number of ways to choose 2 students out of 10 is:
   A) 90 B) 45 C) 20 D) 10
3. What is ?
   A) 18 B) 20 C) 15 D) 10
4. I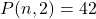f , find n.
   A) 7 B) 8 C) 9 D) 6
5. The probability of getting a head in one toss of a coin is:
   A) 0 B) 1 C) 0.5 D) 2
6. The number of 3-digit numbers formed with digits 1, 2, 3, 4 (without repetition) is:
   A) 12 B) 24 C) 16 D) 36
7. The number of subsets of a set with 5 elements is:
   A) 10 B) 16 C) 25 D) 32
8. is equal to:
   A) 16 B) 28 C) 56 D) 32
9. The number of arrangements of the letters of “MATHS” is:
   A) 60 B) 120 C) 240 D) 720
10. The probability of drawing a king from a deck of 52 cards is:
    A) 1/52 B) 1/26 C) 1/13 D) 4/52

---

5️⃣ ✅ Answer Key (WordPress Table — NO HTML)

Q No | Answer
1 | B
2 | B
3 | B
4 | B
5 | C
6 | B
7 | D
8 | B
9 | B
10 | C

---

6️⃣ 🧠 MCQ Explanations

1️⃣ “ECET” has 4 letters with E repeated twice → → B
2️⃣ → B
3️⃣ → B
4️⃣ → B
5️⃣ Single coin toss → Head or Tail → → C
6️⃣ → B
7️⃣ → D
8️⃣ → B
9️⃣ 5 distinct letters → → B
10️⃣ 4 kings in 52 cards → → C

---

7️⃣ 🎯 Motivation (ECET 2026 Specific)

This topic — Probability, Permutations, and Combinations — appears every single year in ECET!
Scoring in this section boosts your Maths cutoff and overall rank instantly.
Even a single extra correct MCQ here can shift you 300+ ranks higher.
Practice daily small problems — consistency beats last-minute revision!

---

8️⃣ 📲 CTA (Fixed)

Join our ECET 2026 CSE WhatsApp Group for daily quizzes & study notes:
https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9

Download as PDF