Concept Notes (Deep Explanation + Examples)
🔹 Introduction
In surveying, measurements can never be perfect — every reading contains some degree of error. Understanding types of errors and how to adjust them is crucial for accuracy in civil engineering fieldwork and ECET exams.
Surveying deals with measuring distances, angles, and elevations. Any small error here can lead to large positional mistakes in design, mapping, or construction layouts. Hence, knowledge of errors and their adjustments forms the backbone of survey precision.
🔹 1. Definition of Error
An error is the difference between the measured value and the true value of a quantity.
If
then positive error means the measurement is greater, and negative error means it is less than the true value.
🔹 2. Types of Errors in Surveying
(A) Systematic Errors
- Occur due to instrument defects, environmental factors, or observer habits.
- These errors follow a definite pattern and can be corrected mathematically.
Examples:
- Incorrect length of a chain
- Misalignment of the line of sight in a theodolite
- Temperature changes affecting steel tape
Field Example:
If a steel tape expands in summer due to heat, the measured distance will be longer than the actual ground distance unless corrected.
(B) Accidental (Random) Errors
- Occur due to human limitations or observational conditions.
- No fixed pattern — can be reduced by repeated observations and taking mean values.
Example: Reading error while sighting a leveling staff or noting an angle.
(C) Gross Errors
- Mistakes made by surveyors due to carelessness or fatigue.
- Should be detected and eliminated during field checks or office computation.
Example: Miscounting chain links, wrong booking of readings.
🔹 3. Classification of Errors Based on Origin
| Type | Cause | Example |
|---|---|---|
| Instrumental | Defective instrument | Tape not standardized |
| Personal | Observer’s carelessness | Wrong sighting or booking |
| Natural | Environmental effects | Temperature, wind, refraction |
🔹 4. Laws of Errors
- Law of Accidental Errors
Small errors occur more frequently than large ones. - Law of Probability
Positive and negative errors of equal magnitude are equally probable. - Law of Compensation
The algebraic sum of all errors tends to zero if many observations are taken.
🔹 5. Most Probable Value (MPV)
When multiple measurements are taken, the most probable value of a quantity is the mean value, given by:
where
= Mean value
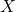= Individual observations
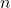= Number of observations
Example:
If 3 observations of a line are 100.02 m, 100.05 m, and 100.03 m
Then,
🔹 6. Theory of Least Squares
Used when several observations are taken with small errors.
The best value is one that minimizes the sum of squares of residuals.
Mathematically,
where 
= residual (difference between observed and adjusted value).
Used in triangulation, leveling networks, GPS adjustments, etc.
🔹 7. Adjustments of Errors
Adjustment means distributing the errors systematically and fairly among the observations.
Types of Adjustments:
- Direct Observation Method:
- Take multiple readings and use their mean.
- Example: Repeating leveling readings for high accuracy.
- Conditional Adjustment:
- Used when observations are connected by conditions (like in a closed traverse).
- Example: In a closed polygon, the sum of included angles = (2n – 4) × 90°
- Graphical & Computational Adjustments:
- Applied using least square methods or balancing traverse by Bowditch rule.
Example (Bowditch Rule):
Correction to latitude or departure:
🔹 Real-World Site Example
In a highway alignment survey, if the traverse does not close perfectly, adjustments are done to balance the traverse.
- Northing/Southing and Easting/Westing errors are distributed based on line length.
- This ensures accurate plotting for construction work.
🔹 Common Mistakes Students Make
- Confusing random and systematic errors.
- Forgetting that gross errors must be eliminated, not adjusted.
- Ignoring temperature and tension corrections in tape measurement.
3️⃣ ⚙️ Formulas (Plain LaTeX Only — No Boxes)
4️⃣ 🔟 10 MCQs (GATE + ECET Mix)
- The difference between measured value and true value is called:
A) Mistake
B) Error
C) Residual
D) Correction - Systematic errors can be:
A) Eliminated by averaging
B) Eliminated by least squares
C) Corrected by mathematical methods
D) Ignored - Random errors are reduced by:
A) Taking one observation
B) Repeating observations and averaging
C) Ignoring large errors
D) Using faulty instruments - Which of the following is a gross error?
A) Temperature change
B) Wrong reading booked
C) Tape not standardized
D) Instrumental defect - The law of accidental errors states:
A) Large errors are common
B) Small errors occur less frequently
C) Small errors occur more frequently
D) All errors are equal - The probable error of a set of observations is proportional to:
A) Mean value
B) Standard deviation
C) Variance
D) Coefficient of correlation - In Bowditch method, correction is proportional to:
A) Length of line
B) Area of traverse
C) Number of sides
D) Included angles - The algebraic sum of errors tends to:
A) Infinity
B) Zero
C) One
D) Undefined - The condition of a closed traverse is:
A) Σ latitude = 0, Σ departure = 0
B) Σ latitude = 1, Σ departure = 1
C) Σ latitude = area, Σ departure = 0
D) Σ latitude = Σ departure - The most probable value of a quantity is:
A) First reading
B) Arithmetic mean
C) Highest reading
D) Lowest reading
5️⃣ ✅ Answer Key
Q.No Answer
1 B
2 C
3 B
4 B
5 C
6 B
7 A
8 B
9 A
10 B
6️⃣ 🧠 Explanations (Step-by-Step)
1️⃣ Error is the difference between measured and true value → ✅ B
2️⃣ Systematic errors are predictable and corrected mathematically → ✅ C
3️⃣ Random errors reduce by repeated observations → ✅ B
4️⃣ Gross error = human mistake (wrong reading booked) → ✅ B
5️⃣ Small errors occur more frequently than large ones → ✅ C
6️⃣ Probable error relates to standard deviation → ✅ B
7️⃣ Bowditch correction ∝ length of line → ✅ A
8️⃣ Algebraic sum of random errors ≈ zero → ✅ B
9️⃣ For a closed traverse: Σ latitude = 0, Σ departure = 0 → ✅ A
10️⃣ Most probable value = arithmetic mean → ✅ B
7️⃣ 🎯 Motivation / Why Practice Matters (ECET 2026 Civil)
“Errors and Adjustments” is a repeated ECET question topic — easy to score if your basics are clear.
Mastering this helps you handle surveying numericals, traverse problems, and adjustment theory confidently.
Remember — surveying is not about remembering; it’s about reasoning.
Stay consistent, revise daily, and your ECET 2026 Civil rank will follow naturally.
8️⃣ 📲 CTA
Join our ECET 2026 Civil WhatsApp Group for daily quizzes & study notes:
👉 https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9
