Why this topic is important for ECET?
In Hydraulics, the concept of flow through pipes is crucial because it forms the base for solving real-world fluid problems like water supply systems, pumping stations, turbines, and pipelines.
In ECET 2026, this topic helps test your conceptual clarity (types of flows, losses, laws) and numerical solving skills (Darcy–Weisbach, continuity, energy equations). Many direct and application-based questions are expected.
📘 Concept Notes
🔹 Types of Flow in Pipes
- Laminar Flow – Fluid particles move in smooth layers (low velocity).
- Reynolds number
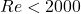. - Example: Oil flowing slowly in thin tubes.
- Reynolds number
- Turbulent Flow – Fluid moves irregularly, with eddies (high velocity).
- Reynolds number
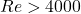. - Example: Water in domestic supply pipes.
- Reynolds number
- Transition Flow – Intermediate, between 2000–4000.
🔹 Continuity Equation
For incompressible fluid,
where 
= discharge, 
= area, 
= velocity.
🔹 Head Loss in Pipes
Fluid flow in pipes causes loss of energy (head) due to friction and fittings.
- Darcy–Weisbach Equation
Minor Losses
- Sudden enlargement:
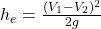
- Sudden contraction:
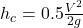
- Bend/valve:
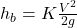
🔹 Power Transmission through Pipe
Maximum power transmitted when
🔹 Pipes in Series and Parallel
- Series: Same discharge 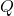, head loss is additive.
- Parallel: Same head loss, discharge divides among pipes.
🔹 Example (Simple)
Water flows through a 200 m long, 0.2 m diameter pipe at 3 m/s. Find head loss (take 
).
⚙️ Formulas
- Reynolds number:
Continuity:
Head loss (Darcy–Weisbach):
Sudden enlargement:
Sudden contraction:
Bend loss:
Power transmitted:
Max power condition:
🔟 10 MCQs
Q1. Reynolds number less than 2000 indicates:
a) Turbulent flow
b) Laminar flow
c) Transition flow
d) None
Q2. For turbulent flow in a pipe, Reynolds number is:
a) <2000
b) 2000–4000
c) >4000
d) 0
Q3. Continuity equation is valid for:
a) Compressible flow only
b) Incompressible flow only
c) Both compressible and incompressible
d) Unsteady flow only
Q4. Head loss due to friction in a pipe varies as:
a)
b) 
c) 
d) 
Q5. Water flows at 3 m/s through a 0.1 m diameter pipe. Discharge is:
a) 0.003 m³/s
b) 0.0236 m³/s
c) 0.00785 m³/s
d) 0.01 m³/s
Q6. Head loss in sudden enlargement is proportional to:
a) latex^2[/latex]
b) latex^2[/latex]
c)
d)
Q7. In parallel pipes, which is constant?
a) Discharge
b) Velocity
c) Head loss
d) Reynolds number
Q8. Maximum power transmitted through a pipe when head loss due to friction equals:
a) H
b) H/2
c) H/3
d) 2H/3
Q9. In Darcy–Weisbach equation, friction factor 
depends on:
a) Flow type & pipe roughness
b) Pipe length
c) Velocity only
d) Pipe material only
Q10. A 0.2 m dia pipe carries water at 2 m/s. What is discharge?
a) 0.0314 m³/s
b) 0.0628 m³/s
c) 0.125 m³/s
d) 0.25 m³/s
✅ Answer Key
| Q | Ans |
|---|---|
| 1 | b |
| 2 | c |
| 3 | c |
| 4 | b |
| 5 | c |
| 6 | b |
| 7 | c |
| 8 | c |
| 9 | a |
| 10 | a |
🧠 Explanations
- Q1: Re < 2000 = laminar → (b).
- Q2: Re > 4000 = turbulent → (c).
- Q3: Continuity applies to all fluids (steady incompressible ideal case) → (c).
- Q4:
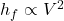→ (b). - Q5:
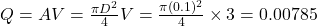→ (c). - Q6: Sudden enlargement loss = latex^2/2g[/latex] → (b).
- Q7: In parallel, head loss same across each pipe → (c).
- Q8: Max power when
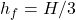→ (c). - Q9: 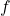depends on flow (laminar/turbulent) & pipe roughness → (a).
- Q10:
→ (a).
🎯 Motivation / Why Practice Matters
Pipe flow questions check formula application + conceptual clarity.
In ECET 2026, time is short, so you need speed (quickly apply equations), accuracy (avoid silly unit mistakes), and edge (attempt extra numericals correctly).
Daily practice ensures you solve pipe flow questions in less than 2 minutes each – which gives a big lead over competitors.
📲 CTA
👉 Join our WHATSAPP group for ECET 2026 updates and discussions:
https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9
