Why this topic is important for ECET
In reinforced concrete design, T-Beams are widely used in floor systems and bridges. In ECET, questions are framed on effective flange width, neutral axis depth, stress distribution, and moment of resistance of T-Beams. A strong grip on this topic helps you tackle both theory and numerical questions quickly, which can give you a competitive edge.
📘 Concept Notes
1. What is a T-Beam?
- A T-beam is a reinforced concrete beam with a cross-section resembling the letter “T”.
- It is formed when a slab and beam act together to resist bending.
- The flange is the slab portion, and the web (rib) is the beam portion.
2. Why T-Beams are needed?
- When beams are cast monolithically with slabs, the slab above the beam resists compression.
- This reduces the amount of reinforcement required in the beam.
- Economical and efficient for multi-storey and bridge decks.
3. Effective Flange Width (IS 456-2000)
The flange width depends on span, beam spacing, and slab thickness.
For a T-beam in a monolithic slab-beam construction, the effective flange width is:
where:
= effective span of the beam
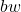= width of the web (rib)
= thickness of the flange (slab)
For an isolated T-beam,
4. Location of Neutral Axis (NA)
- If neutral axis lies within flange → T-beam behaves as a rectangular beam.
- If neutral axis lies below flange → Stress distribution changes, and T-beam formula must be used.
5. Analysis of T-Beams
- Case 1: NA within flange (rectangular section):
Moment of resistance:
Case 2: NA below flange:
Total compressive force = Force in flange + Force in web.
Equating tension and compression, moment capacity is obtained.
6. Design Parameters (as per IS 456-2000)
- Limiting depth of NA for Fe415 steel:
Design stress in steel: 
Balanced design ensures both steel and concrete reach limiting values simultaneously.
7. Example
A T-beam has:
- Web width = 300 mm
- Flange thickness = 120 mm
- Effective flange width = 1500 mm
- Effective depth = 500 mm
- Grade of concrete = M20, Steel = Fe415.
If NA lies within flange, calculate limiting moment of resistance.
Solution:
⚙️ Formulas
🔟 10 MCQs
Q1. In a T-beam, the flange represents:
a) Slab portion
b) Beam portion
c) Reinforcement
d) Neutral axis
Q2. Effective flange width depends on:
a) Grade of steel
b) Beam spacing & slab thickness
c) Load on slab
d) Type of cement
Q3. For Fe415, limiting depth of NA is:
a) 0.53d
b) 0.48d
c) 0.46d
d) 0.42d
Q4. If NA lies within flange, T-beam is treated as:
a) Rectangular beam
b) I-beam
c) Composite beam
d) Trapezoidal beam
Q5. The formula for moment of resistance when NA is within flange is:
a) 
b)
c) 
d) 
Q6. Effective flange width formula (IS 456) is:
a)
b) 
c) 
d) 
Q7. If flange thickness increases, effective flange width:
a) Decreases
b) Increases
c) Constant
d) Independent
Q8. For a beam with bw = 300 mm, D = 100 mm, l0 = 6 m, effective flange width is:
a) 600 mm
b) 1100 mm
c) 1600 mm
d) 2100 mm
Q9. In T-beams, compressive stress is resisted mainly by:
a) Steel reinforcement
b) Flange portion
c) Web portion
d) Entire cross-section equally
Q10. If tension = compression in limit state, which condition is satisfied?
a) Under-reinforced section
b) Balanced section
c) Over-reinforced section
d) Doubly reinforced section
✅ Answer Key
| Q | Answer |
|---|---|
| 1 | a |
| 2 | b |
| 3 | b |
| 4 | a |
| 5 | b |
| 6 | a |
| 7 | b |
| 8 | c |
| 9 | b |
| 10 | b |
🧠 Explanations
- Q1: Flange is slab portion → (a).
- Q2: IS 456 gives formula involving span, web width, slab thickness → (b).
- Q3: For Fe415, xu,lim/d = 0.48 → (b).
- Q4: NA within flange means beam behaves like rectangular → (a).
- Q5: Formula includes flange width bf → (b).
- Q6: Correct IS 456 formula → (a).
- Q7: As D increases, bf increases → (b).
- Q8:
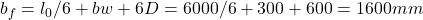→ (c). - Q9: Flange resists compression → (b).
- Q10: Tension = Compression → balanced design → (b).
🎯 Motivation / Why Practice Matters
T-Beams are high scoring because formulas are straightforward but students often confuse effective flange width and NA location. Practicing problems sharpens speed in calculations and improves accuracy in IS 456 provisions. For ECET 2026, solving at least 50+ T-beam problems can give a solid edge over competitors.
📲 CTA
👉 Join our WHATSAPP group for ECET 2026 updates, notes & discussions:
Join Here
