Concept Notes (Deep Explanation + Examples)
🔹 Introduction
In AC circuits, resonance is a very special condition — it’s when the inductive reactance and capacitive reactance become equal in magnitude, cancelling each other out.
In simple words, resonance occurs when the energy exchange between the inductor (L) and capacitor (C) becomes perfectly balanced.
👉 Think of it like a swing — when pushed at the right frequency, it goes higher effortlessly. Similarly, when an AC circuit is driven at its resonant frequency, it performs at its best efficiency.
⚡ Types of Resonance
There are two main types in AC circuits:
- Series Resonance (Voltage Resonance)
- Parallel Resonance (Current Resonance)
Let’s understand both in simple language.
1️⃣ Series Resonance (RLC Series Circuit)
In a series RLC circuit, the same current flows through R, L, and C.
The total impedance is:
At resonance,
So impedance becomes minimum:
That means current is maximum at resonance!
🔹 This is why series resonance is also called current resonance.
📘 Resonant Frequency (f₀):
2️⃣ Parallel Resonance (RLC Parallel Circuit)
In a parallel RLC circuit, current divides into branches.
At resonance, the inductive current and capacitive current are equal and opposite, so they cancel each other.
Hence, total current drawn from supply is minimum.
That means impedance is maximum at resonance.
🔹 Therefore, parallel resonance is also called voltage resonance.
⚙️ Important Characteristics
| Parameter | Series Resonance | Parallel Resonance |
|---|---|---|
| Impedance | Minimum | Maximum |
| Current | Maximum | Minimum |
| Power Factor | Unity | Unity |
| Use | Tuning circuits (radios, filters) | Power systems, filters |
🧩 Quality Factor (Q-Factor)
The Q-Factor indicates the sharpness of resonance.
Higher Q means a narrow and sharp resonance curve (good selectivity).
🧠 Bandwidth (BW)
The bandwidth of a resonant circuit is the range of frequencies around resonance where the power is at least half of the maximum.
🔌 Real-World Analogy
- Resonance in motors: Certain vibration frequencies cause humming — that’s resonance!
- Tuning radio: Adjusting frequency to get clear signal — that’s resonance!
- Electrical panels: Filters use resonance to remove unwanted harmonic frequencies.
🏭 Practical Examples
- In substations: Resonant grounding methods balance neutral voltage.
- In labs: Resonance test is performed using RLC kits.
- In power systems: Capacitor banks and reactors are tuned to avoid resonance with supply frequency (50 Hz).
⚙️ Formulas (Plain LaTeX Only)
🔟 10 MCQs (GATE + ECET Mixed)
- Resonance occurs when
A)
B)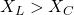
C)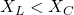
D)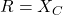
- At resonance in a series RLC circuit, impedance is
A) Maximum
B) Minimum
C) Infinite
D) Zero - Resonant frequency formula is
A)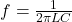
B)
C)
D)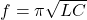
- In parallel resonance, current is
A) Maximum
B) Constant
C) Minimum
D) Zero - Quality factor indicates
A) Power
B) Sharpness of resonance
C) Capacitance value
D) Resistance - Bandwidth formula is
A)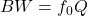
B)
C)
D)
- In series resonance, the power factor is
A) Zero
B) Lagging
C) Unity
D) Leading - When 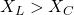, the circuit is
A) Capacitive
B) Resistive
C) Inductive
D) Resonant - For a series RLC circuit, current is maximum at
A) Low frequency
B) High frequency
C) Resonant frequency
D) Zero frequency - In resonance, reactive power is
A) Maximum
B) Zero
C) Minimum
D) Infinite
✅ Answer Key
Q.No Answer
1 A
2 B
3 C
4 C
5 B
6 B
7 C
8 C
9 C
10 B
🧠 MCQ Explanations (Step-by-Step)
1️⃣ At resonance, → both cancel → correct = A
2️⃣ Series resonance → impedance = R (minimum) → correct = B
3️⃣ Resonant frequency = 
→ correct = C
4️⃣ In parallel, opposing branch currents cancel → total current minimum → C
5️⃣ Q-factor = quality or selectivity → B
6️⃣ → B
7️⃣ At resonance, net reactance = 0 → power factor = 1 → C
8️⃣ Inductive reactance dominates → circuit is inductive → C
9️⃣ Current max when impedance min → at f₀ → C
10️⃣ Reactive powers of L and C cancel → total = 0 → B
🎯 Motivation / Why Practice Matters (ECET 2026 EEE)
Resonance is one of the most repeatedly asked topics in ECET & GATE exams.
Understanding it builds a strong base for filters, tuning circuits, and power systems.
Every EEE student must master this because it connects AC theory, machines, and electronics.
Keep practicing — one small topic daily builds a giant result in exams.
🚀 Consistency always beats intensity — one topic a day keeps confusion away!
📲 CTA
Join our ECET 2026 EEE WhatsApp Group for daily quizzes & study notes:
https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9
