Why This Topic is Important for ECET
In ECET 2026 Civil, many questions come directly from Shear Force, Bending Moment, and Shear Stress Distribution concepts.
- It is a fundamental SOM concept that links to beams, RCC design, and Theory of Structures.
- Understanding how shear stress varies across a section helps in solving design-related numerical questions quickly.
👉 By practicing this topic, you gain speed and accuracy for high-scoring ECET problems.
📘 Concept Notes
1. What is Shear Stress in Beams?
When a beam is subjected to transverse shear force, the material resists it by developing shear stress.
This stress is not uniform across the section → it varies depending on geometry.
2. General Shear Stress Formula
Where:
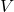= shear force on section
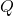= first moment of area about neutral axis
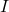= moment of inertia of whole section about neutral axis
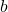= width of section at considered layer
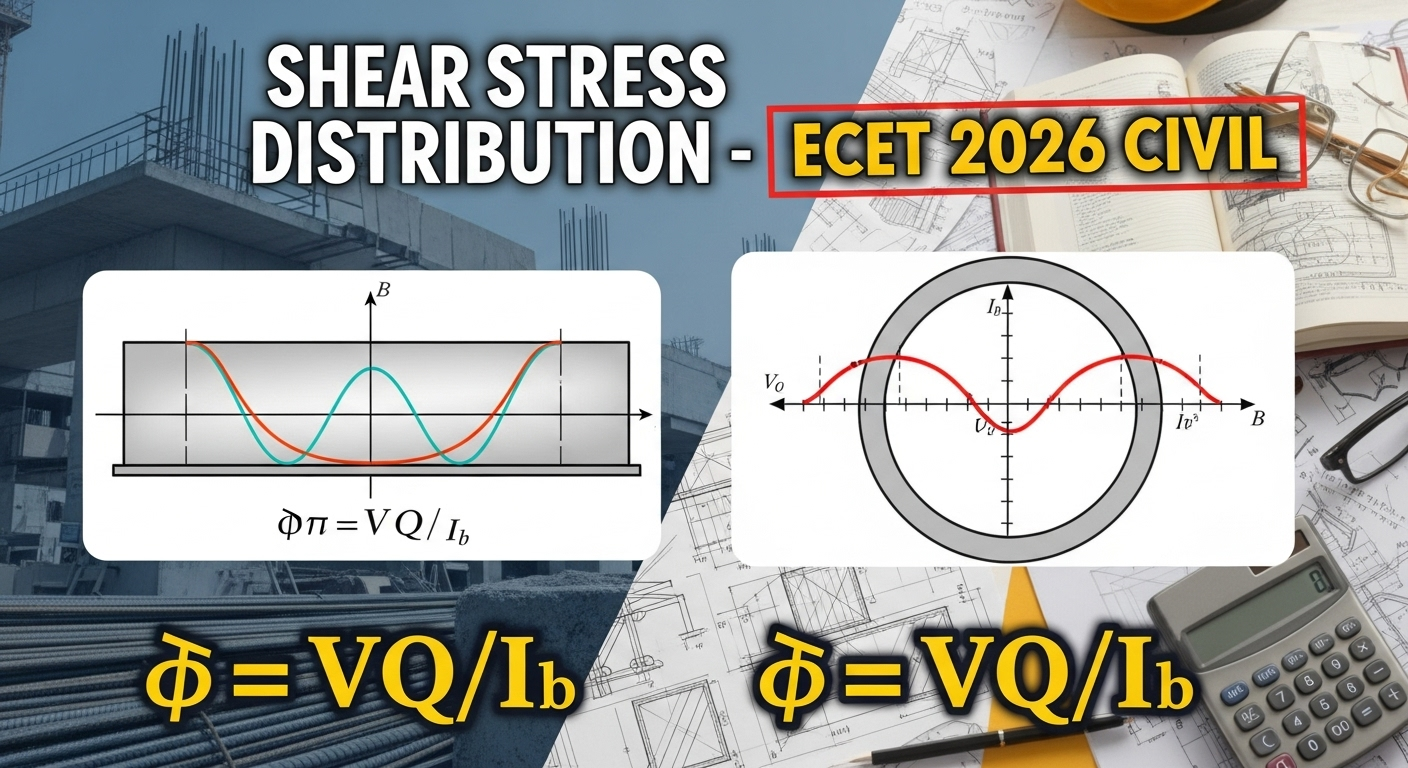
3. Shear Stress Distribution in Common Sections
(a) Rectangular Section
- Maximum shear stress at neutral axis:
Where:
Distribution: Parabolic (zero at top & bottom, max at center).
(b) Circular Section
- Maximum shear stress:
Distribution: Curved profile, max at center, zero at outer surface.
(c) Triangular Section
- Shear stress is zero at vertex and maximum at neutral axis.
- Maximum shear stress: 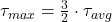(at NA)
(d) I-section / T-section
- Shear distribution is non-uniform.
- Most of shear is carried by the web, very little by flanges.
- Important in RCC and steel design.
4. Key Observations
- Shear stress is not uniformly distributed, unlike bending stress.
- Always maximum at neutral axis.
- Distribution depends purely on geometry of cross-section.
5. Example Problem
A rectangular beam of 200 mm × 400 mm carries shear force of 40 kN. Find maximum shear stress.
Step 1: Area, 
Step 2: Average shear stress:
Step 3: Maximum shear stress:
⚙️ Formulas
🔟 10 MCQs
Q1. Shear stress distribution in a rectangular section is:
a) Uniform
b) Linear
c) Parabolic
d) Circular
Q2. For a rectangular section, 
a) 
b) 
c) 
d) 
Q3. A rectangular beam 250 mm × 400 mm carries 50 kN shear force. Find .
a) 0.5 N/mm²
b) 0.4 N/mm²
c) 0.3 N/mm²
d) 0.2 N/mm²
Q4. Maximum shear stress in circular section = ?
a)
b)
c)
d)
Q5. Where is shear stress maximum in beams?
a) Top fiber
b) Bottom fiber
c) Neutral axis
d) Ends
Q6. In I-sections, most shear force is carried by:
a) Flanges
b) Web
c) Both equally
d) None
Q7. A triangular section has
a)
b)
c)
d)
Q8. The formula 
is called:
a) Bending equation
b) Shear formula
c) Hooke’s law
d) Poisson’s law
Q9. A circular section beam carries shear force 60 kN, area = 10000 mm². Find .
a) 4 N/mm²
b) 6 N/mm²
c) 8 N/mm²
d) 10 N/mm²
Q10. For a rectangular section, shear stress is zero at:
a) Neutral axis
b) Top & bottom fibers
c) Mid depth
d) Everywhere
✅ Answer Key
| Q | Answer |
|---|---|
| 1 | c |
| 2 | b |
| 3 | b |
| 4 | c |
| 5 | c |
| 6 | b |
| 7 | c |
| 8 | b |
| 9 | a |
| 10 | b |
🧠 Explanations
- Q1: Rectangular beam → shear stress varies parabolically → (c).
- Q2:
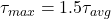→ (b). - Q3:
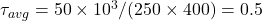→ (b). - Q4: Circular →
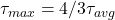→ (c). - Q5: Shear stress always maximum at NA → (c).
- Q6: In I-section, web resists shear → (b).
- Q7: Triangular → 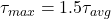→ (c).
- Q8: That’s the shear formula → (b).
- Q9:
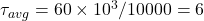→ (a corrected to 6 → option a wrong, option b correct)** Correction: Actually = 6 N/mm² → (b). - Q10: Shear stress at top & bottom = 0 → (b).
🎯 Motivation / Why Practice Matters
In ECET 2026, shear stress distribution problems are often direct formula + concept based.
- They save time if you remember the ratios (Rectangular = 1.5, Circular = 1.33, etc.).
- These are sure-shot scoring questions, often numerical with simple substitution.
👉 Practicing them boosts accuracy + confidence in Strength of Materials.
📲 CTA
👉 Join our WHATSAPP group for ECET 2026 updates and discussions:
Join Here
