
Why This Topic is Important for ECET
Stress and strain form the foundation of Mechanical Design. Every machine element—beams, shafts, bolts, gears—works under forces, and analyzing how materials deform is the first step in safe design.
In ECET 2026, questions on basic mechanics of materials like stress, strain, Hooke’s law, modulus values, and deformation numericals are guaranteed. Mastering this topic gives you confidence in both theory and problem-solving.
📘 Concept Notes
🔹 Stress
- Stress is the internal resisting force per unit area developed inside a material when an external load is applied.
- Formula:
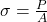
where PPP = Load, AAA = Cross-sectional area.
Types of Stress:
- Tensile Stress → Pulling/stretching force.
- Compressive Stress → Pushing/squeezing force.
- Shear Stress → Tangential force causing sliding.
- Bearing Stress → Contact stress between two surfaces.
🔹 Strain
- Strain is the ratio of deformation to original dimension.
- Formula:

where ΔL\Delta LΔL = change in length, LLL = original length.
Types of Strain:
- Longitudinal Strain → change in length/original length.
- Lateral Strain → change in diameter/original diameter.
- Volumetric Strain → change in volume/original volume.
🔹 Hooke’s Law
- Within elastic limit:
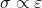
or
Where EEE = Young’s Modulus.
🔹 Elastic Constants
- Young’s Modulus (E) → ratio of stress to strain.
- Shear Modulus (G):
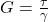
Relation: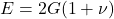
- Bulk Modulus (K):
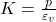
Relation: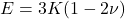
- Poisson’s Ratio (ν):
![]()
🔹 Example
A steel bar of length 2 m and area 200 mm² carries a tensile load of 20 kN.
Stress: ![]()
If E=200 GPaE = 200 \, GPaE=200GPa, Strain = ![]() .
.
Elongation = ![]() .
.
⚙️ Formulas
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
🔟 10 MCQs
Q1. Stress is defined as:
a) Load × Area
b) Load / Area
c) Area / Load
d) None
Q2. Strain is:
a) Dimensionless quantity
b) Has units of N/m²
c) Has units of m²
d) Same as stress
Q3. A bar of length 1 m elongates 1 mm under load. Strain = ?
a) 0.001
b) 0.0001
c) 0.01
d) 1
Q4. If stress = 150 MPa and strain = 0.00075, then E = ?
a) 100 GPa
b) 200 GPa
c) 150 GPa
d) 75 GPa
Q5. The unit of modulus of elasticity is:
a) N
b) Pa (N/m²)
c) m
d) None
Q6. For steel, approximate Poisson’s ratio is:
a) 0.25
b) 0.3
c) 0.5
d) 1.0
Q7. Shear modulus G and E relation is:
a) E = 3G(1–2ν)
b) E = 2G(1+ν)
c) G = 2E(1+ν)
d) E = G/ν
Q8. A bar of length 2 m, cross-section 500 mm² is loaded with 50 kN. Find stress.
a) 100 MPa
b) 50 MPa
c) 200 MPa
d) 25 MPa
Q9. Bulk modulus is defined as:
a) Stress / Strain
b) Pressure / Volumetric strain
c) Shear stress / Shear strain
d) Lateral strain / Longitudinal strain
Q10. When a material is loaded within elastic limit, stress vs strain graph is:
a) Linear
b) Curved
c) Parabolic
d) Horizontal
✅ Answer Key
| Q | Ans |
|---|---|
| 1 | b |
| 2 | a |
| 3 | b |
| 4 | b |
| 5 | b |
| 6 | b |
| 7 | b |
| 8 | a |
| 9 | b |
| 10 | a |
🧠 Explanations
- Q1: Stress = Load/Area → (b).
- Q2: Strain = ΔL/L, ratio → dimensionless → (a).
- Q3: Strain = ΔL/L = 0.001/1 = 0.001 = 0.0001? Careful → 1 mm = 0.001 m, /1 = 0.001 → (b).
- Q4: E = σ/ε = (150×10⁶)/(0.00075) = 200 GPa → (b).
- Q5: E has same units as stress = Pa (N/m²) → (b).
- Q6: Steel ν ≈ 0.3 → (b).
- Q7: Relation E = 2G(1+ν) → (b).
- Q8: Stress = P/A = (50,000)/(500×10⁻⁶) = 100 MPa → (a).
- Q9: K = p/εᵥ → (b).
- Q10: Hooke’s law region = straight line → (a).
🎯 Motivation / Why Practice Matters
Stress & strain concepts are the core of strength of materials and machine design. In ECET 2026, they test your speed in numericals and clarity in concepts.
Practicing MCQs builds quick recall of formulas, sharpens unit conversions, and ensures accuracy under exam pressure.
📲 CTA
👉 Join our WHATSAPP group for ECET 2026 updates and discussions →
https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9



