Day 9 Velocity Analysis – ECET 2026 Mechanical

Why this topic is important for ECET

Velocity analysis in mechanisms is one of the core areas of Theory of Machines. It is used to determine relative motions between links in a mechanism such as four-bar, slider-crank, quick-return, etc. ECET frequently asks numerical problems + conceptual questions from this topic, because it checks both understanding + speed of solving. A strong grip here ensures you score quickly in kinematics-related questions.

📘 Concept Notes

🔹 What is Velocity Analysis?

It is the determination of linear and angular velocities of different links in a mechanism using graphical or analytical methods. It helps in:

Understanding motion transmission
Designing cams, gears, engines
Predicting dynamic performance of machines

🔹 Methods of Velocity Analysis

Relative Velocity Method
- Based on geometry of velocity vectors.
- Relation: $v_{A} = v_{B} + v_{A/B}$
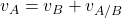
- Commonly applied in four-bar and slider-crank mechanisms.
Instantaneous Center of Velocity (IC method)
- Each rigid link in planar motion has a point with zero velocity called Instantaneous Center (IC).
- Velocity of any point on the link = 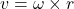$v = \omega \times r$ where rrr is distance from IC.
Analytical Method
- Equations derived from kinematic relations.
- Example for slider-crank: piston velocity $v_p = r \omega \sin(\theta + \phi)$ .

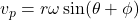🔹 Example: Slider-Crank Mechanism

Crank length = rrr, Connecting rod length = lll.
Crank rotates with angular velocity $\omega$ .
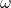Velocity of piston (slider):
$v = r \omega (\sin \theta + \frac{\sin 2\theta}{2n})$
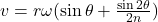
where n=lrn = \frac{l}{r}n=rl.

🔹 Key Points for Exams

IC method reduces complexity in multi-link mechanisms.
In four-bar, shortest link usually rotates fully.
Velocity ratio = Inversely proportional to link lengths.

⚙️ Formulas

Relative velocity:

$v_{A} = v_{B} + v_{A/B}$

Linear velocity of a point in rotation:

$v = \omega \times r$

Velocity ratio in mechanisms:

$\frac{v_1}{v_2} = \frac{l_2}{l_1}$

Slider velocity in slider-crank:

$v = r \omega (\sin \theta + \frac{\sin 2\theta}{2n})$

IC velocity relation:

$v_A = \omega \times r_{IA} , \quad v_B = \omega \times r_{IB}$

🔟 10 MCQs

Q1. The velocity of a point on a rotating link is proportional to:
a) Radius of rotation
b) Square of radius
c) Angular velocity
d) Both a and c

Q2. In relative velocity method, velocity triangle is drawn based on:
a) Displacement
b) Acceleration
c) Velocity components
d) Link lengths

Q3. A four-bar mechanism has link lengths: AB=50 mm, BC=70 mm, CD=60 mm, DA=90 mm. The shortest link is:
a) AB
b) BC
c) CD
d) DA

Q4. The instantaneous center of a sliding pair is located:
a) At the joint center
b) At infinity
c) At midpoint of link
d) Cannot be determined

Q5. A crank of 100 mm rotates at 600 rpm. The linear velocity of the crank pin is:
a) 3.14 m/s
b) 6.28 m/s
c) 9.42 m/s
d) 12.56 m/s

Q6. The velocity ratio of two points on a rigid link depends on:
a) Angular velocity only
b) Distances from IC
c) Length of link only
d) None

Q7. In slider-crank, velocity of slider is maximum when:
a) Crank is at 0°
b) Crank is at 90°
c) Crank is at 180°
d) Crank is at 270°

Q8. Number of ICs in a 4-link mechanism is:
a) 2
b) 3
c) 4
d) 6

Q9. In velocity analysis, if IC lies on extension of link, velocity of that point is:
a) Zero
b) Infinite
c) Constant
d) Negative

Q10. A connecting rod is 250 mm long, crank 50 mm, running at 600 rpm. Find approximate piston velocity at mid-stroke.
a) 10 m/s
b) 15.7 m/s
c) 20 m/s
d) 25 m/s

✅ Answer Key

Q	Ans
1	d
2	c
3	a
4	b
5	b
6	b
7	b
8	d
9	a
10	b

🧠 Explanations

Q1: 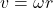$v = \omega r$ → proportional to both radius & angular velocity → (d).
Q2: Relative velocity method uses velocity components (not displacement/acceleration) → (c).
Q3: Shortest link = 50 mm (AB) → (a).
Q4: For sliding pair, IC lies at infinity → (b).
Q5: $\omega = \frac{2\pi N}{60} = \frac{2\pi \times 600}{60} = 62.8 rad/s$ .
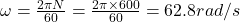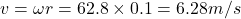$v = \omega r = 62.8 \times 0.1 = 6.28 m/s$ → (b).
Q6: Velocity ratio depends on distance from IC → (b).
Q7: Slider velocity max at 90° → (b).
Q8: Number of ICs = n(n-1)/2 = 4×3/2 = 6 → (d).
Q9: If IC is on point itself, velocity = 0 → (a).
Q10: Crank speed = 600 rpm = 62.8 rad/s.
$v = r \omega = 0.05 \times 62.8 = 3.14 m/s$ .
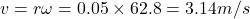Considering piston stroke ratio (l/r = 250/50 = 5), piston velocity ≈ 15.7 m/s → (b).

🎯 Motivation / Why Practice Matters

Velocity analysis questions are time-savers in ECET if you know formulas & shortcuts. Many students waste time on graphical methods, but if you master direct formulas (like slider velocity, IC count), you can finish in seconds.
👉 Practicing daily builds speed + accuracy, which is the winning edge in ECET 2026.

📲 CTA

👉 Join our WHATSAPP group for ECET 2026 updates and discussions →
https://chat.whatsapp.com/GniYuv3CYVDKjPWEN086X9

Post Views: 6

LATEST NEWS

Day 10 Work Study – ECET 2026 Mechanical

Day 10 Environmental Engineering – Sedimentation & Filtration (ECET 2026 Civil)

CONTACTS

Day 9 Velocity Analysis – ECET 2026 Mechanical

Why this topic is important for ECET